题目内容
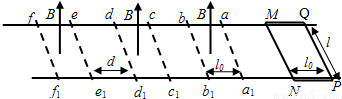
将一质量为m、总电阻为R、长为l、宽为l的矩形线框MNPQ静止搁置在水平平行绝缘导轨上,平行导轨的间距也为l,如图所示.线框与导轨之间的动摩擦因数为μ.在线框左侧的导轨上有一长为l(即aa1=l)、宽度为l、磁感应强度均为B的间隔着分布的相同有界匀强磁场,相邻的磁场区域间距为d(d>l),磁场的边界aa1、bb1垂直于导轨,磁场的方向竖直向上.现用大小为F的拉力水平向左作用在线框,线框恰好能够匀速地穿过磁场区域aa1b1b.若当地的重力加速度为g,求:(1)线框通过aa1b1b磁场区域时的运动速度;(2)F作用前,MN与aa1之间的距离;
(3)线框在通过aa1b1b磁场区域的过程中所生的电热.
【答案】分析:(1)线框在磁场区域做匀速运动时水平方向受拉力、摩擦力、安培力,根据受力平衡列出等式求解.
(2)根据牛顿第二定律求出在进入磁场前,线框的加速度,根据运动学公式求解线框进入磁场前前进的距离.
(3)根据动能定理求得安培力做功,根据安培力做功求出线框在通过aa1b1b磁场区域的过程中所生的电热.
解答:解:(1)线框在磁场区域做匀速运动时,
BIl+μmg=F
感应电流:I=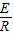
感应电动势:E=Blv
解得匀速运动的速度:v=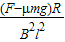
(2)在进入磁场前,线框的加速度
a=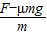
所以线框进入磁场前前进的距离s=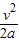 =
=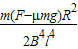
(3)线框在通过磁场的过程中线框通过了2 l的距离,
根据动能定理得:W安+2(F-μmg)l=△Ek=0
所以W安=-2(F-μmg)l,
安培力做功量度电路中产生的内能,所以
Q=-W安=2(F-μmg)l,
答:(1)线框通过aa1b1b磁场区域时的运动速度是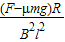 ;
;
(2)F作用前,MN与aa1之间的距离是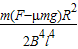 ;
;
(3)线框在通过aa1b1b磁场区域的过程中所生的电热是2(F-μmg)l.
点评:该题考查了多个知识点的综合运用.做这类问题我们应该从运动过程和受力分析入手研究,运用一些物理规律求解问题.
(2)根据牛顿第二定律求出在进入磁场前,线框的加速度,根据运动学公式求解线框进入磁场前前进的距离.
(3)根据动能定理求得安培力做功,根据安培力做功求出线框在通过aa1b1b磁场区域的过程中所生的电热.
解答:解:(1)线框在磁场区域做匀速运动时,
BIl+μmg=F
感应电流:I=
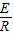
感应电动势:E=Blv
解得匀速运动的速度:v=
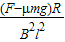
(2)在进入磁场前,线框的加速度
a=
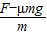
所以线框进入磁场前前进的距离s=
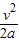 =
=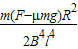
(3)线框在通过磁场的过程中线框通过了2 l的距离,
根据动能定理得:W安+2(F-μmg)l=△Ek=0
所以W安=-2(F-μmg)l,
安培力做功量度电路中产生的内能,所以
Q=-W安=2(F-μmg)l,
答:(1)线框通过aa1b1b磁场区域时的运动速度是
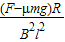 ;
;(2)F作用前,MN与aa1之间的距离是
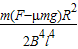 ;
;(3)线框在通过aa1b1b磁场区域的过程中所生的电热是2(F-μmg)l.
点评:该题考查了多个知识点的综合运用.做这类问题我们应该从运动过程和受力分析入手研究,运用一些物理规律求解问题.

练习册系列答案
相关题目



