题目内容
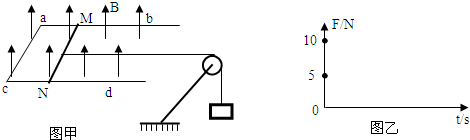
如图甲所示,空间存在竖直向上的磁感应强度为B的匀强磁场,ab、cd是相互平行的间距为l的长直导轨,它们处于同一水平面内,左端由金属丝bc相连,MN是跨接在导轨上质量为m的导体棒,已知MN与bc的总电阻为R,ab、cd的电阻不计.用水平向右的拉力使导体棒沿导轨做匀速运动,并始终保持棒与导轨垂直且接触良好.图乙是棒所受拉力和安培力与时间关系的图象,已知重力加速度为g.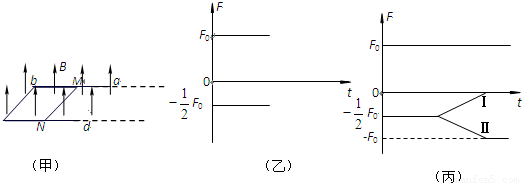
(1)求导体棒与导轨间的动摩擦因数μ;
(2)已知导体棒发生位移s的过程中bc边上产生的焦耳热为Q,求导体棒的电阻值;
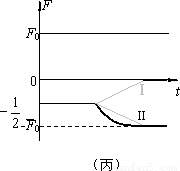
(3)在导体棒发生位移s后轨道变为光滑轨道,此后水平拉力的大小仍保持不变,图丙中Ⅰ、Ⅱ是两位同学画出的导体棒所受安培力随时间变化的图线.判断他们画的是否正确,若正确请说明理由;若都不正确,请你在图中定性画出你认为正确的图线,并说明理由.(要求:说理过程写出必要的数学表达式)
【答案】分析:(1)根据导体棒MN匀速运动时列出平衡等式求解
(2)根据安培力做功量度电路中产生的电能列出等式,根据电阻串联关系求解
(3)应用闭合电路欧姆定律、牛顿运动定律列出等式求解
解答:解:(1)根据导体棒MN匀速运动可知它受牵引力、安培力和摩擦力f三力平衡,
由图象可知拉力大小为F,安培力大小为 F,
F,
根据牛顿第二定律有:F- F-f=0
F-f=0
f=μFN,FN=mg
解得μ=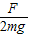
(2)根据功能关系可知导体棒MN克服安培力做功将机械能转化为电能,在电路中电能转化为电热,
电路中的总电热Q总= F?s
F?s
设导体棒的电阻值为r,根据电阻串联关系可知
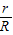 =
=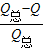
解得r=R(1-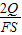 )
)
(3)两位同学画的图线都不正确.
设导体棒运动的速度大小为v,产生的感应电动势为E,感应电流为I
F安=BIl
I=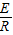
解得F安=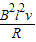
E=Blv
根据牛顿第二定律有F-F安=ma
分析可知随着导体棒加速,安培力F安逐渐增大,加速度逐渐减小.
当F安=F时导体棒将做匀速运动,F安不再变化.
其变化过程如图所示.
答:(1)导体棒与导轨间的动摩擦因数是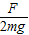 ;
;
(2)已知导体棒发生位移s的过程中bc边上产生的焦耳热为Q,导体棒的电阻值是R(1-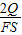 );
);
(3)两位同学画的图线都不正确,如上图.
点评:解决该题关键要应用法拉第电磁感应定律、闭合电路欧姆定律、牛顿运动定律、平衡条件及其相关知识列方程解答.
(2)根据安培力做功量度电路中产生的电能列出等式,根据电阻串联关系求解
(3)应用闭合电路欧姆定律、牛顿运动定律列出等式求解
解答:解:(1)根据导体棒MN匀速运动可知它受牵引力、安培力和摩擦力f三力平衡,
由图象可知拉力大小为F,安培力大小为
 F,
F,根据牛顿第二定律有:F-
 F-f=0
F-f=0f=μFN,FN=mg
解得μ=
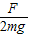
(2)根据功能关系可知导体棒MN克服安培力做功将机械能转化为电能,在电路中电能转化为电热,
电路中的总电热Q总=
 F?s
F?s设导体棒的电阻值为r,根据电阻串联关系可知
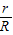 =
=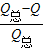
解得r=R(1-
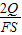 )
)(3)两位同学画的图线都不正确.
设导体棒运动的速度大小为v,产生的感应电动势为E,感应电流为I
F安=BIl
I=
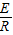
解得F安=
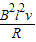
E=Blv
根据牛顿第二定律有F-F安=ma
分析可知随着导体棒加速,安培力F安逐渐增大,加速度逐渐减小.
当F安=F时导体棒将做匀速运动,F安不再变化.
其变化过程如图所示.

答:(1)导体棒与导轨间的动摩擦因数是
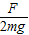 ;
;(2)已知导体棒发生位移s的过程中bc边上产生的焦耳热为Q,导体棒的电阻值是R(1-
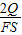 );
);(3)两位同学画的图线都不正确,如上图.
点评:解决该题关键要应用法拉第电磁感应定律、闭合电路欧姆定律、牛顿运动定律、平衡条件及其相关知识列方程解答.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
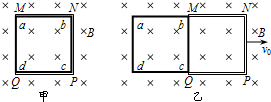 (2006?泰州模拟)如图甲所示,空间存在着一个范围足够大的竖直向下的匀强磁场,磁场的磁感强度大小为B.边长为l的正方形金属框abcd(下简称方框)放在光滑的水平地面上,其外侧套着一个与方框边长相同的U形金属框架MNPQ(下简称U形框),U形框与方框之间接触良好且无摩擦.两个金属框每条边的质量均为m,每条边的电阻均为r.
(2006?泰州模拟)如图甲所示,空间存在着一个范围足够大的竖直向下的匀强磁场,磁场的磁感强度大小为B.边长为l的正方形金属框abcd(下简称方框)放在光滑的水平地面上,其外侧套着一个与方框边长相同的U形金属框架MNPQ(下简称U形框),U形框与方框之间接触良好且无摩擦.两个金属框每条边的质量均为m,每条边的电阻均为r.
 如图甲所示,空间存在着以x=0平面为理想分界面的两个匀强磁场,左右两边磁场的磁感应强度分别为B1和B2,且B1:B2=4:3.方向如图,现在原点O处有一静止的中性粒子,突然分裂成两个带电粒子a和b,已知a带正电荷,分裂时初速度方向沿x轴正方向.若a粒子在第4次经过y轴时,恰与b粒子相遇.(1)在图乙中,画出a粒子的运动轨迹及用字母c标出a、b两粒子相遇的位置
如图甲所示,空间存在着以x=0平面为理想分界面的两个匀强磁场,左右两边磁场的磁感应强度分别为B1和B2,且B1:B2=4:3.方向如图,现在原点O处有一静止的中性粒子,突然分裂成两个带电粒子a和b,已知a带正电荷,分裂时初速度方向沿x轴正方向.若a粒子在第4次经过y轴时,恰与b粒子相遇.(1)在图乙中,画出a粒子的运动轨迹及用字母c标出a、b两粒子相遇的位置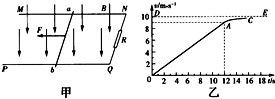 如图甲所示,空间存在B=0.5T、方向竖直向下的匀强磁场,MN、PQ是相互平行的粗糙的长直导轨,它们处于同一水平面内,其间距L=0.2m,R是连在导轨一端的电阻,ab是跨接在导轨上质量m=0.1kg的导体棒,从零时刻开始,通过一小型电动机对ab棒施加一个牵引力F,方向水平向左,使其从静止开始沿导轨做直线运动,此过程中棒始终保持与导轨垂直且接触良好,图乙是棒的速度一时间图象,其中OA段是直线,AC段是曲线,DE是曲线图象的渐近线,小型电动机在12s末达到额定功率P=4.5W,此后功率保持不变.导体棒和导轨的电阻均不计,g取10m/s2.
如图甲所示,空间存在B=0.5T、方向竖直向下的匀强磁场,MN、PQ是相互平行的粗糙的长直导轨,它们处于同一水平面内,其间距L=0.2m,R是连在导轨一端的电阻,ab是跨接在导轨上质量m=0.1kg的导体棒,从零时刻开始,通过一小型电动机对ab棒施加一个牵引力F,方向水平向左,使其从静止开始沿导轨做直线运动,此过程中棒始终保持与导轨垂直且接触良好,图乙是棒的速度一时间图象,其中OA段是直线,AC段是曲线,DE是曲线图象的渐近线,小型电动机在12s末达到额定功率P=4.5W,此后功率保持不变.导体棒和导轨的电阻均不计,g取10m/s2.