题目内容
13. 在某一旅游景区,建有一山坡滑草运动项目.该山坡可看成倾角θ=30°的斜面,一名游客连同滑草装置总质量m=80kg,他从静止开始无动力匀加速下滑,在时间t=5s内沿斜面滑下的位移s=50m.(不计空气阻力,取g=10m/s2).求:(答案可保留根号)
在某一旅游景区,建有一山坡滑草运动项目.该山坡可看成倾角θ=30°的斜面,一名游客连同滑草装置总质量m=80kg,他从静止开始无动力匀加速下滑,在时间t=5s内沿斜面滑下的位移s=50m.(不计空气阻力,取g=10m/s2).求:(答案可保留根号)(1)游客下滑的加速度;
(2)滑草装置与草皮之间的动摩擦因数μ;
(3)设游客滑下50m后进入水平草坪,游客在水平面上滑动的最大距离.(滑草装置与草皮间的动摩擦因数处处相同).
分析 (1)根据匀变速直线运动的位移时间公式求出下滑的加速度.
(2)对物体进行受力分析,根据牛顿第二定律求出下滑过程中的摩擦力.滑草装置在垂直于斜面方向合力等于零,求出支持力的大小,根据F=μFN求出滑草装置与草皮之间的动摩擦因数μ.
(3)先由位移速度公式求出游客到达最低点的速度,然后又牛顿第二定律求出加速度,最后由位移速度公式求出位移.
解答 解:(1)由运动学公式:$s=\frac{1}{2}a{t}^{2}$,
代入数据解得:a=4m/s2
(2)沿斜面方向,由牛顿第二定律得:
mgsinθ-f=ma
在垂直斜面方向上:
N-mgcosθ=0
又f=μN
联立,代入数据解得:μ=$\frac{\sqrt{3}}{15}$
(3)取水平向右为正方向,下滑50m后的速度,由vt=v0+at
可得:vt=20m/s
在水平面上:-μmg=ma′
代入数据得:$a′=-\frac{2\sqrt{3}}{3}m/{s}^{2}$
到游客停止时,$2a′s′=v{′}_{t}^{2}-{v}_{t}^{2}$
代入数据解得:$s=100\sqrt{3}$m
答:(1)游客连同滑草装置在下滑过程中的加速度a的大小为2m/s2;
(2)滑草装置与草皮之间的动摩擦因数μ为$\frac{\sqrt{3}}{15}$.
(3)游客在水平面上滑动的最大距离是100$\sqrt{3}$m.
点评 解决本题的关键知道加速度是联系力学和运动学的桥梁,通过加速度可以根据力求运动,也可以根据运动求力.

练习册系列答案
相关题目
4.表为某电热水壶铭牌上的一部分内容.根据表中的信息,可计算出电热水壶在额定电压下以额定功率工作时的电流约为多少?
| 型 号 | DF-938 | 额定功率 | 900W |
| 额定电压 | 220V | 额定容量 | 1.2L |
1.关于匀加速直线运动,下列说法中正确的是( )
| A. | 加速度不断变大的运动 | B. | 位移随时间均匀变化的运动 | ||
| C. | 加速度不变的运动 | D. | 速度随时间均匀变化的运动 |
8. 两位同学进行竞走比赛,她们分别拿着底部穿孔、滴水比较均匀的饮料瓶,假设每隔1s漏下一滴,她们在平直路上行走,同学们根据漏在地上的水印分布,分析她们的行走情况(已知人的运动方向).下列说法中正确的是 ( )
两位同学进行竞走比赛,她们分别拿着底部穿孔、滴水比较均匀的饮料瓶,假设每隔1s漏下一滴,她们在平直路上行走,同学们根据漏在地上的水印分布,分析她们的行走情况(已知人的运动方向).下列说法中正确的是 ( )
 两位同学进行竞走比赛,她们分别拿着底部穿孔、滴水比较均匀的饮料瓶,假设每隔1s漏下一滴,她们在平直路上行走,同学们根据漏在地上的水印分布,分析她们的行走情况(已知人的运动方向).下列说法中正确的是 ( )
两位同学进行竞走比赛,她们分别拿着底部穿孔、滴水比较均匀的饮料瓶,假设每隔1s漏下一滴,她们在平直路上行走,同学们根据漏在地上的水印分布,分析她们的行走情况(已知人的运动方向).下列说法中正确的是 ( )| A. | 当沿运动方向水印间距逐渐增大时,人一定是做匀加速直线运动 | |
| B. | 当沿运动方向水印始终均匀分布时,人可能做匀速直线运动 | |
| C. | 当沿运动方向水印间距逐渐增大时,人的速度可能在减小 | |
| D. | 当沿运动方向水印间距逐渐增大时,人的加速度可能在增大 |
18.一个物体做匀速圆周运动,在运动过程中一定不发生变化的物理量是( )
| A. | 角速度 | B. | 速度 | C. | 加速度 | D. | 合外力 |
5.关于一对作用力和反作用力,下列说法正确的是( )
| A. | 它们的方向相同 | B. | 它们作用在同一物体上 | ||
| C. | 它们的大小相等 | D. | 先有作用力,后才有反作用力 |
2.一物体在粗糙地面上以一定的初速度匀减速滑动,若已知物体在第1s内位移为8.0m,在第3s内位移为0.5m,则下列说法正确的是( )
| A. | 物体的加速度大小一定为4.0m/s2 | B. | 物体的加速度大小一定为3.75m/s2 | ||
| C. | 物体在第0.5s末速度一定为8.0m/s | D. | 物体在第2.5s末速度一定为0.5m/s |

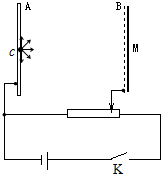 如图所示,在铅板A中心处有个放射源C,它能向各个方向不断地射出速度大小相等的电子流,B为金属网,M为紧靠B外侧的荧光屏.A和B接在电路中,它们相互平行且正对面积足够大.已知电源电动势为E,滑动变阻器的最大电阻是电源内阻的8倍,A、B间距为d且固定不动,电子质量为m,电量为e,不计电子形成的电流对电路的影响,忽略重力的作用.
如图所示,在铅板A中心处有个放射源C,它能向各个方向不断地射出速度大小相等的电子流,B为金属网,M为紧靠B外侧的荧光屏.A和B接在电路中,它们相互平行且正对面积足够大.已知电源电动势为E,滑动变阻器的最大电阻是电源内阻的8倍,A、B间距为d且固定不动,电子质量为m,电量为e,不计电子形成的电流对电路的影响,忽略重力的作用.