题目内容
如图,不可伸长的轻质细绳跨过光滑的轻质滑轮,绳两端各系一小球.a球质量为m,静止于地面;b球质量为3m,用手托住,高度为h,此时绳刚好拉紧.从静止开始释放b,a上升的最大高度为 .(a球不会碰到滑轮)
【答案】分析:本题分为两个过程来求解,b球落地之前:首先根据ab系统的机械能守恒,可以求得a球上升h时的速度的大小;b球落地之后:a球的机械能守恒,从而可以求得a球上升的高度的大小.
解答:解:设a球到达高度h时两球的速度V,b球落地之前,根据系统机械能守恒得:
3mgh=mgh+ ?(3m+m)V2
?(3m+m)V2
解得 两球的速度都为V=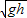 ,
,
b球落地之后:绳子松驰,a球开始做初速为V=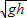 的竖直上抛运动,
的竖直上抛运动,
根据机械能守恒:mgh+ mV2=mgH
mV2=mgH
解得a球能达到的最大高度H=1.5h.
故答案为: h
h
点评:在a球上升的全过程中,a球的机械能是不守恒的,所以在本题中要分过程来求解,第一个过程系统的机械能守恒,在第二个过程中只有a球的机械能守恒.
解答:解:设a球到达高度h时两球的速度V,b球落地之前,根据系统机械能守恒得:
3mgh=mgh+
 ?(3m+m)V2
?(3m+m)V2解得 两球的速度都为V=
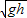 ,
,b球落地之后:绳子松驰,a球开始做初速为V=
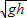 的竖直上抛运动,
的竖直上抛运动,根据机械能守恒:mgh+
 mV2=mgH
mV2=mgH解得a球能达到的最大高度H=1.5h.
故答案为:
 h
h点评:在a球上升的全过程中,a球的机械能是不守恒的,所以在本题中要分过程来求解,第一个过程系统的机械能守恒,在第二个过程中只有a球的机械能守恒.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,不可伸长的轻质细绳跨过光滑的轻质滑轮,绳两端各系一小球.a球质量为m,静止于地面;b球质量为3m,用手托住,高度为h,此时绳刚好拉紧.从静止开始释放b,a上升的最大高度为
如图,不可伸长的轻质细绳跨过光滑的轻质滑轮,绳两端各系一小球.a球质量为m,静止于地面;b球质量为3m,用手托住,高度为h,此时绳刚好拉紧.从静止开始释放b,a上升的最大高度为 和
和 的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的摩擦.设细绳对A和B的拉力大小分别为
的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的摩擦.设细绳对A和B的拉力大小分别为 和
和 已知下列四个关于
已知下列四个关于




 和
和 的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的摩擦.设细绳对A和B的拉力大小分别为
的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的摩擦.设细绳对A和B的拉力大小分别为 和
和 已知下列四个关于
已知下列四个关于
 B.
B.
 D.
D.
