题目内容
9. 如图所示,光滑的水平轨道与光滑半圆弧轨道相切.圆轨道半径R=2.5m,一质量m=1kg的小球停放在光滑水平轨道上,现给小球一个v0=5$\sqrt{5}$m/s的初速度,小球恰能通过最高点C后落回A点,不计空气阻力,g=10m/s2求:
如图所示,光滑的水平轨道与光滑半圆弧轨道相切.圆轨道半径R=2.5m,一质量m=1kg的小球停放在光滑水平轨道上,现给小球一个v0=5$\sqrt{5}$m/s的初速度,小球恰能通过最高点C后落回A点,不计空气阻力,g=10m/s2求:(1)球过B点时对半圆轨道的压力;
(2)AB两点间的水平距离;
(3)球落到A点时的速度.
分析 (1)根据牛顿第二定律,结合径向的合力提供向心力求出小球在B点所受的支持力,从而得出压力的大小.
(2)根据动能定理求出C点的速度,根据高度求出平抛运动的时间,结合初速度和时间求出水平位移.
(3)根据平抛运动的规律,结合平行四边形定则求出球落到A点的速度大小.
解答 解:(1)根据牛顿第二定律得,${N}_{B}-mg=m\frac{{{v}_{0}}^{2}}{R}$,
解得${N}_{B}=mg+m\frac{{{v}_{0}}^{2}}{R}=10+1×\frac{125}{2.5}$N=60N.
根据牛顿第三定律知,球过B点时对半圆轨道的压力为60N.
(2)根据动能定理得,$-mg•2R=\frac{1}{2}m{{v}_{C}}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$,
代入数据解得vC=5m/s,
根据$2R=\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{4R}{g}}=\sqrt{\frac{4×2.5}{10}}s=1s$,
则AB间的水平距离x=vCt=5×1m=5m.
(3)根据平行四边形定则知,落到A点的速度${v}_{A}=\sqrt{{{v}_{C}}^{2}+2g•2R}=\sqrt{25+20×5}$m/s=$5\sqrt{5}$m/s.
答:(1)球过B点时对半圆轨道的压力为60N;
(2)AB两点间的水平距离为5m;
(3)球落到A点时的速度为$5\sqrt{5}$m/s.
点评 本题考查了圆周运动和平抛运动的基本运用,掌握圆周运动向心力的来源,以及平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
19.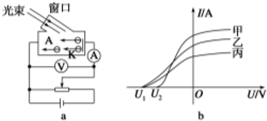 在光电效应实验中,小明同学用同一实验装置(如图a)在甲、乙、丙三种光的照射下得到了三条电流表与电压表读数之间的关系曲线,如图b所示.则不正确的是( )
在光电效应实验中,小明同学用同一实验装置(如图a)在甲、乙、丙三种光的照射下得到了三条电流表与电压表读数之间的关系曲线,如图b所示.则不正确的是( )
 在光电效应实验中,小明同学用同一实验装置(如图a)在甲、乙、丙三种光的照射下得到了三条电流表与电压表读数之间的关系曲线,如图b所示.则不正确的是( )
在光电效应实验中,小明同学用同一实验装置(如图a)在甲、乙、丙三种光的照射下得到了三条电流表与电压表读数之间的关系曲线,如图b所示.则不正确的是( )| A. | 乙光的频率小于甲光的频率 | |
| B. | 甲光的波长大于丙光的波长 | |
| C. | 丙光的光子能量小于甲光的光子能量 | |
| D. | 乙光对应的光电子最大初动能小于丙光的光电子最大初动能 |
17.关于电场线,下列说法中正确的是( )
| A. | 电场线是电场中实际存在的一些曲线 | |
| B. | 匀强电场的电场线是一组相互平行等间距的直线 | |
| C. | 两条电场线在电场中可以交于一点 | |
| D. | 电场线起始于负电荷,终止于正电荷 |
4.若单摆的摆长不变,摆球的质量增大为原来的4倍,摆球经过平衡位置时的速度减小为原来的一半,则单摆振动的( )
| A. | 频率增大 | B. | 频率减小 | C. | 振幅增大 | D. | 振幅减小 |
1.弹簧一端固定,另一端受到拉力F 的作用,F与弹簧伸长量x的关系如图所示.该弹簧的劲度系数为( )

| A. | 2 N/m | B. | 4 N/m | C. | 20 N/m | D. | 0.05 N/m |
 为验证向心力公式,某探究小组设计了如图所示的演示实验,在米尺的一端钻一个小孔,使小孔恰能穿过一根细线,线下端挂一可视为质点,质量为m.将米尺固定在水平桌面上,测量出悬点到钢球的细线长度l,使钢球在水平面内做匀速圆周运动,圆心为O,待钢球的运动稳定后,用眼睛从米尺上方垂直于米尺往下看,读出钢球外侧到O点的距离r,并用秒表测量出钢球转动n圈用的时间t.则:
为验证向心力公式,某探究小组设计了如图所示的演示实验,在米尺的一端钻一个小孔,使小孔恰能穿过一根细线,线下端挂一可视为质点,质量为m.将米尺固定在水平桌面上,测量出悬点到钢球的细线长度l,使钢球在水平面内做匀速圆周运动,圆心为O,待钢球的运动稳定后,用眼睛从米尺上方垂直于米尺往下看,读出钢球外侧到O点的距离r,并用秒表测量出钢球转动n圈用的时间t.则: 如图所示,由某种透明物质制成的直角三棱镜ABC,折射率n=3,∠A=30°.一束与BC面成30°角的光线从O点射入棱镜,从AC面上O′点射出.不考虑光在BC面上的反射,求从O′点射出的光线的方向.
如图所示,由某种透明物质制成的直角三棱镜ABC,折射率n=3,∠A=30°.一束与BC面成30°角的光线从O点射入棱镜,从AC面上O′点射出.不考虑光在BC面上的反射,求从O′点射出的光线的方向. 如图,A、B两物体叠放在一起,由静止释放后沿光滑固定斜面下滑,下滑过程中A、B始终保持相对静止,B上表面水平,则物体B的受力示意图是( )
如图,A、B两物体叠放在一起,由静止释放后沿光滑固定斜面下滑,下滑过程中A、B始终保持相对静止,B上表面水平,则物体B的受力示意图是( )


