题目内容
如图所示，一高度为h=0.8m粗糙的水平面在B点处与一倾角为θ=30°光滑的斜面BC连接，一小滑块从水平面上的A点以v0=3m/s的速度在粗糙的水平面上向右运动。运动到B点时小滑块恰能沿光滑斜面下滑。已知AB间的距离s=5m，求：（1）小滑块与水平面间的动摩擦因数；
（2）小滑块从A点运动到地面所需的时间；
（3） 若小滑块从水平面上的A点以v1=5m/s的速度在粗糙的水平面上向右运动，运动到B点时小滑块将做什么运动？并求出小滑块从A点运动到地面所需的时间。（取g=10m/s2）。
解：（1）小滑块运动到B点时速度恰为零，设小滑块在水平面上运动的加速度大小为a，据牛顿第二定律可得 μmg=ma （3分）由运动学公式得 
（2分）解得 
（2分）（2）小滑块运动到B点t1=
=3.3s （2分）在斜面上运动的时间 t2=
（2分）小滑块从A点运动到地面所需的时间为 t=t1+t2=4.1s （1分）（3）若小滑块从水平面上的A点以v1=5m/s的速度在粗糙的水平面上向右运动，运动到B点时的速度为，由
得vB=
4m/s （2分）小滑块将做平抛运动。 假设小滑块不会落到斜面上，则经过
， （2分）由于水平运动的位移x=vBt3=1.67m>
=1.36m所以假设正确。 （2分）小滑块从A点运动到地面所需的时间为
s （2分）
（2分）解得 （2分）（2）小滑块运动到B点t1==3.3s （2分）在斜面上运动的时间 t2= （2分）小滑块从A点运动到地面所需的时间为 t=t1+t2=4.1s （1分）（3）若小滑块从水平面上的A点以v1=5m/s的速度在粗糙的水平面上向右运动，运动到B点时的速度为，由 得vB=4m/s （2分）小滑块将做平抛运动。 假设小滑块不会落到斜面上，则经过， （2分）由于水平运动的位移x=vBt3=1.67m>=1.36m所以假设正确。 （2分）小滑块从A点运动到地面所需的时间为s （2分） 
练习册系列答案
精英口算卡系列答案
相关题目
如图所示，一高度为h=0.8m粗糙的水平面在B点处与一倾角为θ=30°光滑的斜面BC连接，一小滑块从水平面上的A点以v0=3m/s的速度在粗糙的水平面上向右运动．运动到B点时小滑块恰能沿光滑斜面下滑．已知AB间的距离s=5m，求：
（2003?上海）如图所示，一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接，一小球以v0=5m/s的速度在平面上向右运动．求小球从A点运动到地面所需的时间（平面与斜面均光滑，取g=10m/s2）．某同学对此题的解法为：小球沿斜面运动，则
如图所示，一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接，一小球以v0=5m/s的速度在平面上向右运动，求小球从A点运动到地面所需的时间（平面与斜面均光滑，取g=10m/s2）．
（2011?皇姑区一模）如图所示，一高度为h的光滑水平面与一倾角为θ的斜面在P点连接，该斜面在Q点处与地面连接．一小球以速度v在光滑水平面上向右运动．则小球经过P点后一段时间内（ ）
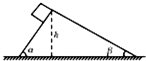如图所示，一高度为h的楔形物块固定在水平地面上，质量为m的物体由静止开始从倾角分别为α、β的两个光滑斜面的顶端滑下，则下列说法中正确的是（ ）| A、物体滑到斜面底端的速度相同 | B、物体滑到斜面底端所用的时间相同 | C、物体滑到斜面底端时重力所做功的功率相同 | D、物体滑到斜面底端过程中重力所做的功相同 |