题目内容
16.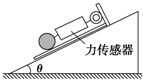 一足够长的倾角为θ的斜面固定在水平面上,在斜面顶端放置一长木板,木板与斜面之间的动摩擦因数为μ,木板上固定一力传感器,连接传感器和光滑小球间是一平行于斜面的轻杆,如图所示,现由静止释放木板,木板沿斜面下滑,稳定时传感器的示数为F1,当木板固定时,传感器的示数为F2.则下列说法正确的是( )
一足够长的倾角为θ的斜面固定在水平面上,在斜面顶端放置一长木板,木板与斜面之间的动摩擦因数为μ,木板上固定一力传感器,连接传感器和光滑小球间是一平行于斜面的轻杆,如图所示,现由静止释放木板,木板沿斜面下滑,稳定时传感器的示数为F1,当木板固定时,传感器的示数为F2.则下列说法正确的是( )| A. | 稳定后传感器的示数一定为零 | B. | tan θ=$\frac{μ{F}_{1}}{{F}_{2}}$ | ||
| C. | cot θ=$\frac{{F}_{1}}{μ{F}_{2}}$ | D. | cot θ=$\frac{{F}_{2}}{μ{F}_{1}}$ |
分析 当木板沿斜面下滑时,对整体分析,求出加速度,隔离对小球分析,求出传感器示数的表达式,当木板固定时,对小球分析,根据共点力平衡求出传感器示数的表达式,从而分析判断.
解答 解:当木板沿斜面下滑时,对整体分析,加速度a=gsinθ-μgcosθ,
隔离对小球分析,mgsinθ-F1=ma,解得F1=μmgcosθ,
当木板固定时,对小球分析,根据共点力平衡有:F2=mgsinθ,
则$\frac{{F}_{1}}{{F}_{2}}=\frac{μcosθ}{sinθ}$,解得$cotθ=\frac{{F}_{1}}{μ{F}_{2}}$.故C正确,A、B、D错误.
故选:C.
点评 本题考查了共点力平衡和牛顿第二定律的基本运用,掌握整体法和隔离法的灵活运用,知道木板沿斜面下滑时,小球和木板具有相同的加速度.

练习册系列答案
相关题目
6. 空间某区域存在一电场,一带负电的粒子仅在电场力作用下从x1处沿x轴负方向运动.粒子质量为m,初速度大小为v0,其电势能Ep随坐标x变化的关系如图所示,图线关于纵轴左右对称,以无穷远处为零电势能点,粒子在原点0处电势能为E0,在x1处电势能为E1,则下列说法中正确的是( )
空间某区域存在一电场,一带负电的粒子仅在电场力作用下从x1处沿x轴负方向运动.粒子质量为m,初速度大小为v0,其电势能Ep随坐标x变化的关系如图所示,图线关于纵轴左右对称,以无穷远处为零电势能点,粒子在原点0处电势能为E0,在x1处电势能为E1,则下列说法中正确的是( )
 空间某区域存在一电场,一带负电的粒子仅在电场力作用下从x1处沿x轴负方向运动.粒子质量为m,初速度大小为v0,其电势能Ep随坐标x变化的关系如图所示,图线关于纵轴左右对称,以无穷远处为零电势能点,粒子在原点0处电势能为E0,在x1处电势能为E1,则下列说法中正确的是( )
空间某区域存在一电场,一带负电的粒子仅在电场力作用下从x1处沿x轴负方向运动.粒子质量为m,初速度大小为v0,其电势能Ep随坐标x变化的关系如图所示,图线关于纵轴左右对称,以无穷远处为零电势能点,粒子在原点0处电势能为E0,在x1处电势能为E1,则下列说法中正确的是( )| A. | 坐标原点0处两侧电场方向相同 | |
| B. | 由x1运动到0过程电场力做负功 | |
| C. | 粒子经过x1、-x1处速度不相同 | |
| D. | 若粒子能够沿x轴负方向运动越过0点,一定有v0>$\sqrt{\frac{2({E}_{0}-{E}_{1})}{m}}$ |
7. 如图所示,平行虚线之间有垂直于纸面向里的匀强磁场,磁场左右宽度为L,磁感应强度大小为B.一等腰梯形线圈ABCD所在平面与磁场垂直,AB边刚好与磁场右边界重合.AB长等于L,CD长等于2L,AB、CD间的距离为2L,线圈的电阻为R.现让线圈向右以恒定速度v匀速运动,从线圈开始运动到CD边刚好要进入磁场的过程中( )
如图所示,平行虚线之间有垂直于纸面向里的匀强磁场,磁场左右宽度为L,磁感应强度大小为B.一等腰梯形线圈ABCD所在平面与磁场垂直,AB边刚好与磁场右边界重合.AB长等于L,CD长等于2L,AB、CD间的距离为2L,线圈的电阻为R.现让线圈向右以恒定速度v匀速运动,从线圈开始运动到CD边刚好要进入磁场的过程中( )
 如图所示,平行虚线之间有垂直于纸面向里的匀强磁场,磁场左右宽度为L,磁感应强度大小为B.一等腰梯形线圈ABCD所在平面与磁场垂直,AB边刚好与磁场右边界重合.AB长等于L,CD长等于2L,AB、CD间的距离为2L,线圈的电阻为R.现让线圈向右以恒定速度v匀速运动,从线圈开始运动到CD边刚好要进入磁场的过程中( )
如图所示,平行虚线之间有垂直于纸面向里的匀强磁场,磁场左右宽度为L,磁感应强度大小为B.一等腰梯形线圈ABCD所在平面与磁场垂直,AB边刚好与磁场右边界重合.AB长等于L,CD长等于2L,AB、CD间的距离为2L,线圈的电阻为R.现让线圈向右以恒定速度v匀速运动,从线圈开始运动到CD边刚好要进入磁场的过程中( )| A. | 线圈中感应电流沿顺时针方向 | B. | 线圈中感应电动势大小为BLv | ||
| C. | 通过线圈截面的电量为$\frac{B{L}^{2}}{2R}$ | D. | 克服安培力做的功为$\frac{{{B^2}{L^3}v}}{4R}$ |
4.下列说法正确的是( )
| A. | 笛卡儿指出:如果运动中的物体没有受到力的作用,它将继续以同一速度沿同一直线运动,既不停下来也不偏离原来的方向 | |
| B. | 用比值法定义的物理概念在物理学中占有相当大的比例,例如场强E=$\frac{F}{q}$,电容C=$\frac{Q}{U}$,加速度a=$\frac{F}{m}$ 都是采用比值法定义的 | |
| C. | 卡文迪许测出了引力常量的数值,库仑测出了静电力常量的数值 | |
| D. | 法拉第根据小磁针在通电导线周围的偏转,发现了电流的磁效应 |
11.下列说法正确的是( )
| A. | 我们在地球上接收到来自遥远星球的光波的波长变长,可以判断该星球正在离我们远去 | |
| B. | 为了从高频电流中取出所携带的声音信号就要进行调制 | |
| C. | 用光导纤维束传输图象和信息,这是利用了光的全反射原理 | |
| D. | 根据麦充斯韦的电磁场理论,变化的电场一定可以产生电磁波 | |
| E. | 利用红外摄影可以不受天气(阴雨、大雾等)的影响,因为红外线比可见光波长长,更容易绕过障碍物 |
1.以下说法正确的是( )
| A. | 一定质量的气体,在体积不变时,分子每秒与器壁平均碰撞次数随着温度降低而减小 | |
| B. | 晶体熔化时吸收热量,分子平均动能一定增大 | |
| C. | 知道水蒸气的摩尔体积和水分子的体积,可计算出阿伏加德罗常数 | |
| D. | 当分子间的引力和斥力平衡时,分子势能最小 |
5. 如图所示的电路中,电源电动势为E、内阻忽略不计,ab是总电阻为2R的滑动变阻器,滑片P刚开始位于中间位置,定值电阻的阻值为R,平行板电容器的电容为C,其下极板与地(取为零电势)相连,一电量为q带正电的粒子固定在两板中央e处,闭合开关S,待稳定后,下列判断正确的是( )
如图所示的电路中,电源电动势为E、内阻忽略不计,ab是总电阻为2R的滑动变阻器,滑片P刚开始位于中间位置,定值电阻的阻值为R,平行板电容器的电容为C,其下极板与地(取为零电势)相连,一电量为q带正电的粒子固定在两板中央e处,闭合开关S,待稳定后,下列判断正确的是( )
 如图所示的电路中,电源电动势为E、内阻忽略不计,ab是总电阻为2R的滑动变阻器,滑片P刚开始位于中间位置,定值电阻的阻值为R,平行板电容器的电容为C,其下极板与地(取为零电势)相连,一电量为q带正电的粒子固定在两板中央e处,闭合开关S,待稳定后,下列判断正确的是( )
如图所示的电路中,电源电动势为E、内阻忽略不计,ab是总电阻为2R的滑动变阻器,滑片P刚开始位于中间位置,定值电阻的阻值为R,平行板电容器的电容为C,其下极板与地(取为零电势)相连,一电量为q带正电的粒子固定在两板中央e处,闭合开关S,待稳定后,下列判断正确的是( )| A. | e处的电势为$\frac{1}{6}$E | |
| B. | 若把滑片P移至b端,稳定后粒子的电势能减少了$\frac{1}{3}$Eq | |
| C. | 若把滑片P移至b端,稳定后粒子所受电场力变为原来的2倍 | |
| D. | 若把滑片P移至b端,同时上极板向上移动仅使板间距变为原来的2倍,稳定后电容器的带电量变为原来的1.5倍 |
 如图所示,光滑水平面上有大小相同的A、B两球,mA=1kg,mB=2kg,A、B两球有一被压缩弹簧,弹簧被细线锁定.现烧断细线解除锁定弹开小球,B球获得的动量大小为4kg•m/s,若规定向右为正方向,求
如图所示,光滑水平面上有大小相同的A、B两球,mA=1kg,mB=2kg,A、B两球有一被压缩弹簧,弹簧被细线锁定.现烧断细线解除锁定弹开小球,B球获得的动量大小为4kg•m/s,若规定向右为正方向,求 如图所示,小物块A、B由跨过定滑轮的轻绳相连,A置于倾角为37°的光滑固定斜面上,B位于水平传送带的左端,轻绳分别与斜面、传送带平行.传送带始终以速度v0=2m/s顺时针匀速传动,某时刻B从传送带左端以速度v1=6m/s向右运动,经一段时间回到传送带的左端.已知A、B质量均为1kg,B与传送带间的动摩擦因数为μ=0.2,斜面、轻绳、传送带均足够长,A不会碰到定滑轮,定滑轮的质量与摩擦均不计.g取10m/s2,sin37°=0.6.求:
如图所示,小物块A、B由跨过定滑轮的轻绳相连,A置于倾角为37°的光滑固定斜面上,B位于水平传送带的左端,轻绳分别与斜面、传送带平行.传送带始终以速度v0=2m/s顺时针匀速传动,某时刻B从传送带左端以速度v1=6m/s向右运动,经一段时间回到传送带的左端.已知A、B质量均为1kg,B与传送带间的动摩擦因数为μ=0.2,斜面、轻绳、传送带均足够长,A不会碰到定滑轮,定滑轮的质量与摩擦均不计.g取10m/s2,sin37°=0.6.求: