题目内容
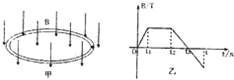
如图甲所示,在整个矩形区域MNPQ内有由M指向N方向的匀强电场E(图甲中未画出)和垂直矩形区域向外的匀强磁场B(图甲中未画出),E和B随时间变化的规律如图乙所示在t=0时刻,将带正电、比荷为25C/kg的粒子从MQ的中点无初速释放,粒子在第8s内经NP边离开矩形区域已知MQ边足够长,粒子重力不计,
=0.32.
(1)求矩形区域PQ边长满足的条件;
(2)若要粒子从MQ边飞出,释放粒子的时刻t应满足什么条件?
| 1 | π |

(1)求矩形区域PQ边长满足的条件;
(2)若要粒子从MQ边飞出,释放粒子的时刻t应满足什么条件?
分析:(1)带电粒子在电场中做匀加速直线运动,在磁场中做匀速圆周运动.根据牛顿第二定律和运动学公式得到前7s内粒子的位移.再根据条件:第8s内从NP边离开矩形区域,由几何关系分析矩形区域PQ边长满足的条件;
(2)由运动学公式求出粒子在电场中运动的总时间表达式,由洛伦兹力提供向心力得到磁场中运动的轨迹半径,根据粒子要从MQ边飞出半径与位移的关系,求解释放粒子的时刻t应满足的条件.
(2)由运动学公式求出粒子在电场中运动的总时间表达式,由洛伦兹力提供向心力得到磁场中运动的轨迹半径,根据粒子要从MQ边飞出半径与位移的关系,求解释放粒子的时刻t应满足的条件.
解答: 解:(1)第1s内粒子在电场力的作用下作匀加速直线运动,设加速度为a,由牛顿第二定律有:
解:(1)第1s内粒子在电场力的作用下作匀加速直线运动,设加速度为a,由牛顿第二定律有:
a=
①
第2s内粒子在库仑力作用下作匀速圆周运动,
有:T=
②
代入已知数据可得:T=1s,所以可得粒子在1s、3s、5s、7s内作匀加速运动,2s,4s,6s内作匀速圆周运动.
可作出粒子在第8s内刚好不从NP边离开矩形区域的运动示意图,如图所示.粒子在奇数秒内的整体运动可以等效为初速度为0的匀加速直线运动.
设前7s内的位移为s7,s7=
a(7-3)2 ③
设粒子第7s末的速度为υ7,第8s内粒子圆周运动的半径为R8,有:
υ7=a(7-3),
qυ7B=m
④
由图可知,粒子要在第8s内从NP边离开矩形区域,要满足s7<LNP<s7+R8 ⑤
由以上各式联立求解,可得:8m<LNP<8.64m;
(2)设在第1秒内的t0时刻释放粒子,则第1s内粒子在电场力的作用下加速时间为1-t0,第1s内的位移为s0,第1s末的速度大小为υ0,由运动学方程有:s0=
a(1-t0)2 ⑥
υ0=a(1-t0) ⑦
粒子在磁场中作匀速圆周运动,设圆周运动的半径为r0,有:qυ0B=m
⑧
要粒子从MQ边界飞出,则r0>s0⑨
由⑥~⑨式可得:t>0.68s;
结合电场和磁场的周期性可得要粒子从MN边飞出,粒子释放的时刻t满足:(2n+0.68)s<t<(2n+1)s (n∈N).
答:
(1)矩形区域PQ边长满足的条件是:8m<LNP<8.64m;
(2)若要粒子从MQ边飞出,释放粒子的时刻t应满足的条件是:(2n+0.68)s<t<(2n+1)s (n∈N).
 解:(1)第1s内粒子在电场力的作用下作匀加速直线运动,设加速度为a,由牛顿第二定律有:
解:(1)第1s内粒子在电场力的作用下作匀加速直线运动,设加速度为a,由牛顿第二定律有:a=
| qE |
| m |
第2s内粒子在库仑力作用下作匀速圆周运动,
有:T=
| 2πm |
| qB |
代入已知数据可得:T=1s,所以可得粒子在1s、3s、5s、7s内作匀加速运动,2s,4s,6s内作匀速圆周运动.
可作出粒子在第8s内刚好不从NP边离开矩形区域的运动示意图,如图所示.粒子在奇数秒内的整体运动可以等效为初速度为0的匀加速直线运动.
设前7s内的位移为s7,s7=
| 1 |
| 2 |
设粒子第7s末的速度为υ7,第8s内粒子圆周运动的半径为R8,有:
υ7=a(7-3),
qυ7B=m
| υ72 |
| R8 |
由图可知,粒子要在第8s内从NP边离开矩形区域,要满足s7<LNP<s7+R8 ⑤
由以上各式联立求解,可得:8m<LNP<8.64m;
(2)设在第1秒内的t0时刻释放粒子,则第1s内粒子在电场力的作用下加速时间为1-t0,第1s内的位移为s0,第1s末的速度大小为υ0,由运动学方程有:s0=
| 1 |
| 2 |
υ0=a(1-t0) ⑦
粒子在磁场中作匀速圆周运动,设圆周运动的半径为r0,有:qυ0B=m
| ||
| r0 |
要粒子从MQ边界飞出,则r0>s0⑨
由⑥~⑨式可得:t>0.68s;
结合电场和磁场的周期性可得要粒子从MN边飞出,粒子释放的时刻t满足:(2n+0.68)s<t<(2n+1)s (n∈N).
答:
(1)矩形区域PQ边长满足的条件是:8m<LNP<8.64m;
(2)若要粒子从MQ边飞出,释放粒子的时刻t应满足的条件是:(2n+0.68)s<t<(2n+1)s (n∈N).
点评:分析粒子的受力情况,判断其运动情况是解决本题的基础,关键要画出轨迹,运用几何关系分析相关的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 2004年1月,我国月球探测工程经国务院正式批准立项后,该工程被命名为“嫦娥工程”,整个探月工程将分为三期完成,要突破“绕”、“落”和“回”三大关键技术.第一颗绕月卫星命名为“嫦娥一号”,并且“嫦娥二号”于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空,并获得了圆满成功.
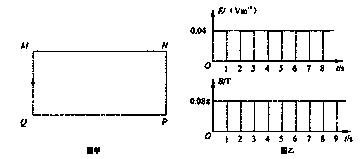
2004年1月,我国月球探测工程经国务院正式批准立项后,该工程被命名为“嫦娥工程”,整个探月工程将分为三期完成,要突破“绕”、“落”和“回”三大关键技术.第一颗绕月卫星命名为“嫦娥一号”,并且“嫦娥二号”于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空,并获得了圆满成功. 如图甲所示,在一个正方形金属线圈区域内,存在着磁感应强度B随时间变化的匀强磁场,磁场的方向与线圈平面垂直.金属线圈所围的面积S=200cm2,匝数n=1000,线圈电阻r=1.0Ω.线圈与电阻R构成闭合回路,电阻的阻值R=4.0Ω.匀强磁场的磁感应强度随时间变化的情况如图乙所示,求:
如图甲所示,在一个正方形金属线圈区域内,存在着磁感应强度B随时间变化的匀强磁场,磁场的方向与线圈平面垂直.金属线圈所围的面积S=200cm2,匝数n=1000,线圈电阻r=1.0Ω.线圈与电阻R构成闭合回路,电阻的阻值R=4.0Ω.匀强磁场的磁感应强度随时间变化的情况如图乙所示,求: