题目内容
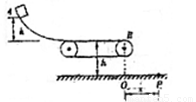
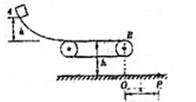
 如图所示,带弧形轨道的小车放在上表面光滑、静止浮于水面的船上,车左端被固定在船上的物体挡住,小车的弧形轨道和水平部分在B点相切,且AB段光滑,BC段粗糙.现有一个离车的BC面高为h的木块由A点从静止滑下,最终停在车面上BC段的某处.已知木块、车、船的质量分别为m1=m、m2=2m、m3=3m;木块与车表面间的动摩擦因素μ=0.4,水对船的阻力不计,求木块在BC面上滑行的距离S是多少?(设船足够长)
如图所示,带弧形轨道的小车放在上表面光滑、静止浮于水面的船上,车左端被固定在船上的物体挡住,小车的弧形轨道和水平部分在B点相切,且AB段光滑,BC段粗糙.现有一个离车的BC面高为h的木块由A点从静止滑下,最终停在车面上BC段的某处.已知木块、车、船的质量分别为m1=m、m2=2m、m3=3m;木块与车表面间的动摩擦因素μ=0.4,水对船的阻力不计,求木块在BC面上滑行的距离S是多少?(设船足够长)分析:对木块、小车、小车组成的系统,运用机械能守恒和水平方向上动量守恒求出木块运动到B点时物块的速度和船与车的共同速度,当车停止在BC段上时,结合动量守恒定律和能量守恒定律求出木块在BC面上滑行的距离.
解答:解:A到B,由木块、小车、小船构成的系统机械能守恒,水平方向动量守恒.
设:木块在B点时,木块的速度为v1(向右),船与小车的共同速度为v2(向左):mgh=
m
+
×5m
①
mv1=5mv2 ②
解①、②得:v1=
,v2=
木块在BC间滑动时,由木块、小车组成的系统水平方向动量守恒,能量守恒.设该系统最终的共同速度为v3,以v1的方向为正方向.
根据动量守恒定律得,mv1-2mv2=3mv3 ③
根据能量守恒定律得,
m
+
2m
-
3m
=μmgs ④
解③、④得s=
h.
答:木块在BC面上滑行的距离S是
.
设:木块在B点时,木块的速度为v1(向右),船与小车的共同速度为v2(向左):mgh=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
mv1=5mv2 ②
解①、②得:v1=
|
|
木块在BC间滑动时,由木块、小车组成的系统水平方向动量守恒,能量守恒.设该系统最终的共同速度为v3,以v1的方向为正方向.
根据动量守恒定律得,mv1-2mv2=3mv3 ③
根据能量守恒定律得,
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 3 |
解③、④得s=
| 16 |
| 15 |
答:木块在BC面上滑行的距离S是
| 16h |
| 15 |
点评:本题综合考查了动量守恒定律和能量守恒定律,以及机械能守恒定律,综合性较强,对学生的能力要求较高,需加强这方面的训练.

练习册系列答案
相关题目