题目内容
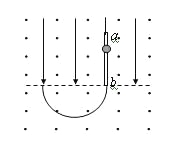
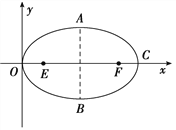
【题目】如图所示，光滑绝缘半圆环轨道放在竖直向下的匀强电场中，场强为E.在与环心等高处放有一质量为m、带电荷量＋q的小球，由静止开始沿轨道运动，下列说法正确的是（ ）
A.小球在运动过程中机械能恒定B.小球经过环的最低点时速度最大
C.小球由静止释放到达最低点，电势能增加EqRD.小球由静止释放到达最低点，动能的增量等于mgR
【答案】B
【解析】
A．小球运动过程中电场力做功，机械能不守恒，故A错误；
B．小球所受的电场力竖直向下，从最高点到最低点的过程中，合力做正功，则根据动能定理得知，动能增大，速度增大，所以小球经过环的最低点时速度最大，故B正确；
CD．小球从最高点到最低点的过程，根据动能定理得：
（mg+qE）R=△Ek
电场力做功W=EqR，所以电势能减小qER，动能的增加量等于（mg+qE）R，故CD错误；
故选B。
练习册系列答案
相关题目
