题目内容
宇宙间存在一些离其他恒星较远的三星系统.其中有一种三星系统如图所示,三颗质量均为m的星体位于等边三角形的三个顶点上,三角形边长为R.忽略其他星体对它们的引力作用,三星在同一平面内绕三角形中心O做匀速圆周运动,引力常量为G.则( )
A.每颗星做圆周运动的线速度为

B.每颗星做圆周运动的角速度为

C.每颗星做圆周运动的周期为2

D.每颗星做圆周运动的加速度与三星的质量无关
【答案】分析:先写出任意两个星星之间的万有引力,求每一颗星星受到的合力,该合力提供它们的向心力.
然后用R表达出它们的轨道半径,最后写出用周期和线速度表达的向心力的公式,整理即可的出结果.
解答:解:A、任意两个星星之间的万有引力F=
每一颗星星受到的合力,F1= F
F
由几何关系知:它们的轨道半径r= R①
R①
合力提供它们的向心力: =
= ②
②
联立①②,解得:v= ,故A正确
,故A正确
C、 =
=
解得:T= ,故C错误
,故C错误
B、角速度ω= =
= ,故B错误
,故B错误
D、 =ma
=ma
a= ,故加速度与它们的质量有关.故D错误
,故加速度与它们的质量有关.故D错误
故选A.
点评:解决该题首先要理解模型所提供的情景,然后能够列出合力提供向心力的公式,才能正确解答题目.
然后用R表达出它们的轨道半径,最后写出用周期和线速度表达的向心力的公式,整理即可的出结果.
解答:解:A、任意两个星星之间的万有引力F=

每一颗星星受到的合力,F1=
 F
F由几何关系知:它们的轨道半径r=
 R①
R①合力提供它们的向心力:
 =
= ②
②联立①②,解得:v=
 ,故A正确
,故A正确C、
 =
=
解得:T=
 ,故C错误
,故C错误B、角速度ω=
 =
= ,故B错误
,故B错误D、
 =ma
=maa=
 ,故加速度与它们的质量有关.故D错误
,故加速度与它们的质量有关.故D错误故选A.
点评:解决该题首先要理解模型所提供的情景,然后能够列出合力提供向心力的公式,才能正确解答题目.

练习册系列答案
相关题目
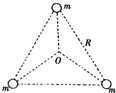 宇宙间存在一些离其他恒星较远的三星系统.其中有一种三星系统如图所示,三颗质量均为m的星体位于等边三角形的三个顶点上,三角形边长为R.忽略其他星体对它们的引力作用,三星在同一平面内绕三角形中心O做匀速圆周运动,引力常量为G.则( )
宇宙间存在一些离其他恒星较远的三星系统.其中有一种三星系统如图所示,三颗质量均为m的星体位于等边三角形的三个顶点上,三角形边长为R.忽略其他星体对它们的引力作用,三星在同一平面内绕三角形中心O做匀速圆周运动,引力常量为G.则( )


