题目内容
2.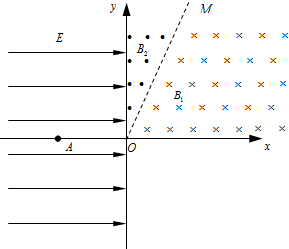 如图所示,在第一象限内有垂直纸面向里和向外的匀强磁场,磁感应强度分别为B1=0.1T、B2=0.05T,分界线OM与x轴正方向的夹角为α.在第二、三象限内存在着沿x轴正方向的匀强电场,电场强度E=1×104V/m.现有一带电粒子由x轴上A点静止释放,从O点进入匀强磁场区域.已知A点横坐标xA=-5×10-2m,带电粒子的质量m=1.6×10-24kg,电荷量q=+1.6×10-15C.
如图所示,在第一象限内有垂直纸面向里和向外的匀强磁场,磁感应强度分别为B1=0.1T、B2=0.05T,分界线OM与x轴正方向的夹角为α.在第二、三象限内存在着沿x轴正方向的匀强电场,电场强度E=1×104V/m.现有一带电粒子由x轴上A点静止释放,从O点进入匀强磁场区域.已知A点横坐标xA=-5×10-2m,带电粒子的质量m=1.6×10-24kg,电荷量q=+1.6×10-15C.(1)要使带电粒子能始终在第一象限内运动,求α的取值范围?(用反三角函数表示)
(2)如果α=30°,则粒子能经过OM分界面上的哪些点?
(3)如果α=30°,让粒子在OA之间的某点释放,要求粒子仍能经过(2)问中的那些点,则粒子释放的位置应满足什么条件?
分析 带电粒子在组合场中的运动问题,首先要运用动力学方法分析清楚粒子的运动情况.粒子在电场中做匀加速直线运动,根据直线运动公式求出粒子进入磁场的速度.粒子在磁场中圆周运动,根据磁场强度的关系,求出半径值比,正确画出轨迹,由几何知识及三角函数求解.
解答 解:(1)粒子进入匀强磁场后,做匀速圆周运动.设在B1中运动的半径为r1,在B2中运动的半径为r2,
由$qvB=m\frac{v^2}{r}$
B1=2 B2
得 r2=2r1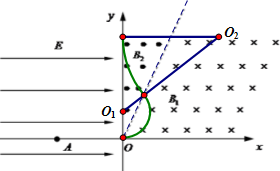
由几何关系解得 $α<\frac{π}{2}-\frac{1}{2}arcsin\frac{2}{3}$
(2)当α=30°时,粒子每次在任意一个磁场中运动的圆弧的圆心角均为60°,弦长均等于半径.
粒子在电场中运动 $qE{x_A}=\frac{1}{2}m{v^2}$
粒子在磁场中运动 ${r_1}=\frac{mv}{{q{B_1}}}$
解得:
${r_1}=1×{10^{-2}}m$
${r_2}=2{r_1}=2×{10^{-2}}m$
OM上经过的点距离O点的距离是$l=k{r_1}+(k-1){r_2}=(3k-2){r_1}=(3k-2)×{10^{-2}}m$(k=1、2、3…)
或 $l=k'({r_1}+{r_2})=3k'×{10^{-2}}m$(k′=1、2、3…)
(3)要仍然经过原来的点,需满足 ${r_1}=n({r_1}^′+{r_2}^′)$(n=1、2、3…)
解得 $r'=\frac{r_1}{3n}$即$v'=\frac{v}{3n}$
粒子释放的位置应满足 ${x_A}^′=\frac{x_A}{{9{n^2}}}$(n=1、2、3…)
或者 ${r_1}=n'(2{r_1}^{′′}+{r_2}^{′′})$(n′=1、2、3…)
解得,$r''=\frac{r_1}{4n'}$即$v''=\frac{v}{4n'}$
粒子释放的位置应满足${x_A}^{′′}=\frac{x_A}{{16{{n'}^2}}}$(n′=1、2、3…)
答:(1)要使带电粒子能始终在第一象限内运动,求α的取值范围为$α<\frac{π}{2}-\frac{1}{2}arcsin\frac{2}{3}$;
(2)如果α=30°,则粒子能经过OM分界面上的哪些点(3k-2)×10-2m(k=1、2、3…)或3k′×10-2(k′=1、2、3…);
(3)如果α=30°,让粒子在OA之间的某点释放,要求粒子仍能经过(2)问中的那些点,则粒子释放的位置应满足${x}_{A}^{′}=\frac{{x}_{A}}{{9n}^{2}}$或${x}_{A}^{″}=\frac{{x}_{A}}{16{{n}^{′}}^{2}}$.
点评 此题考查了粒子在复合场中的运动,需考生熟练掌握圆周运动的公式及应用.首先根据题意,画出粒子的运动轨迹,找到临界值,求出角度.根据草图找出粒子经过哪些点,通过分析得出数学规律.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 氡的半衰期为3.8天,若取8个氡原子核,经7.6天后就一定剩下2个原子核了 | |
| B. | 原子核内的中子转化成一个质子和一个电子,这种转化产生的电子发射到核外,就是β粒子,这就是β衰变的实质 | |
| C. | 光子的能量由光的频率所决定 | |
| D. | 只要有核反应发生,就一定会释放出核能 | |
| E. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,电势能增大,原子的总能量增加 |
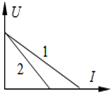
| A. | 当I1=I2时,电源总功率P1=P2 | |
| B. | 当I1=I2时,外电阻R1>R2 | |
| C. | 当U1=U2时,电源输出功率P出1<P出2 | |
| D. | 当U1=U2时,电源内部消耗的电功率P内1>P内2 |
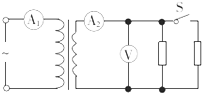 图示是一理想变压器的电路连接图,变压器原线圈两端加有正弦交变电压,副线圈接有两个定值电阻,当开关S闭合到断开时,各理想电表示数的变化是( )
图示是一理想变压器的电路连接图,变压器原线圈两端加有正弦交变电压,副线圈接有两个定值电阻,当开关S闭合到断开时,各理想电表示数的变化是( )| A. | 电流表 、 、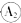 的示数变小,电压表 的示数变小,电压表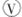 的示数变大 的示数变大 | |
| B. | 电流表 、 、 的示数变小,电压表 的示数变小,电压表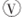 的示数不变 的示数不变 | |
| C. | 电流表 、 、 的示数变小,电压表 的示数变小,电压表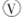 的示数变小 的示数变小 | |
| D. | 电流表 、 、 的示数变大,电压表 的示数变大,电压表 的示数变大 的示数变大 |
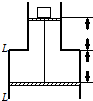 如图所示的装置,气缸分上、下两部分,下部分的横截面积大于上部分的横截面积,大小活塞分别在上、下气缸内用一根硬杆相连,两活塞可在气缸内一起上下移动.缸内封有一定质量的气体,活塞与缸壁无摩擦且不漏气,起初,在小活塞上的杯子里放有大量钢球,请问哪些情况下能使两活塞相对气缸向下移动( )
如图所示的装置,气缸分上、下两部分,下部分的横截面积大于上部分的横截面积,大小活塞分别在上、下气缸内用一根硬杆相连,两活塞可在气缸内一起上下移动.缸内封有一定质量的气体,活塞与缸壁无摩擦且不漏气,起初,在小活塞上的杯子里放有大量钢球,请问哪些情况下能使两活塞相对气缸向下移动( )| A. | 给气缸内气体缓慢加热 | B. | 取走几个钢球 | ||
| C. | 大气压变大 | D. | 让整个装置自由下落 |
 如图所示,氢原子从n>2的某一能级跃迁到n=2的能级,辐射出能量为2.55eV的光子,则最少要给基态的氢原子提供多少电子伏特的能量,才能使它辐射上述能量的光子( )
如图所示,氢原子从n>2的某一能级跃迁到n=2的能级,辐射出能量为2.55eV的光子,则最少要给基态的氢原子提供多少电子伏特的能量,才能使它辐射上述能量的光子( )| A. | 0.85 eV | B. | 2.55 eV | C. | 12.75 eV | D. | 13.6 eV |
 如图,有一理想变压器,原、副线圈的匝数比为n1:n2,原线圈接正弦交流电压,电压的最大值为U,输出端接有一个理想交流电流表和一个电动机.电动机线圈电阻为R.当输入端接通电源后,电流表读数为I,电动机带动一质量为m的重物以速度v匀速上升.下列判断正确的是( )
如图,有一理想变压器,原、副线圈的匝数比为n1:n2,原线圈接正弦交流电压,电压的最大值为U,输出端接有一个理想交流电流表和一个电动机.电动机线圈电阻为R.当输入端接通电源后,电流表读数为I,电动机带动一质量为m的重物以速度v匀速上升.下列判断正确的是( )| A. | 原线圈中的电流的最大值为$\frac{{n}_{2}I}{{n}_{1}}$ | |
| B. | 电动机两端电压为$\frac{{n}_{2}U}{\sqrt{2}{n}_{1}}$ | |
| C. | 电动机消耗的功率为mgv | |
| D. | 理想变压器的输入功率为$\frac{{n}_{2}UI}{\sqrt{2}{n}_{1}}$ |

| A. | 有效值 | B. | 频率 | C. | 最大值 | D. | 均不一样 |
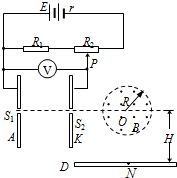 如图所示为一个自动控制装置的工作原理简图.在电路中,电源电动势E=91V,内阻r=1.0Ω,定值电阻R1=10Ω,滑动变阻器R2的最大阻值为80Ω.在以O为圆心,半径为R=10$\sqrt{3}$cm的圆形区域内,有一个方向垂直纸面向外的水平匀强磁场,磁感应强度大小为B=0.10T.竖直平行放置的两金属板A、K相距为d,S1、S2为A、K板上的两个小孔,且S1、S2跟O在竖直极板的同一直线上,OS2=2R,另有一水平放置的足够长的荧光屏D,O点跟荧光屏D点之间的距离为H.比荷为2.0×105C/kg的离子流由S1进入电场后,通过S2向磁场中心射去,通过磁场后落到荧光屏D上.离子进入电场的初速度、重力、离子之间的作用力均可忽略不计.问:
如图所示为一个自动控制装置的工作原理简图.在电路中,电源电动势E=91V,内阻r=1.0Ω,定值电阻R1=10Ω,滑动变阻器R2的最大阻值为80Ω.在以O为圆心,半径为R=10$\sqrt{3}$cm的圆形区域内,有一个方向垂直纸面向外的水平匀强磁场,磁感应强度大小为B=0.10T.竖直平行放置的两金属板A、K相距为d,S1、S2为A、K板上的两个小孔,且S1、S2跟O在竖直极板的同一直线上,OS2=2R,另有一水平放置的足够长的荧光屏D,O点跟荧光屏D点之间的距离为H.比荷为2.0×105C/kg的离子流由S1进入电场后,通过S2向磁场中心射去,通过磁场后落到荧光屏D上.离子进入电场的初速度、重力、离子之间的作用力均可忽略不计.问: