题目内容
如图，甲、乙两小球质量分别为m1、m2，m2=2m1，两球之间连接了一根轻弹簧，用一段轻绳将甲球系在天花板上．现在烧断细绳的瞬间，甲、乙球加速度分别为a1、a2，则（ ）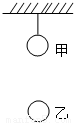
A．a1=g
B．a1=3g
C．a2=0
D．a2=g
【答案】分析：细绳烧断的瞬间，弹簧的弹力不变，根据牛顿第二定律求出瞬时加速度的大小．
解答：解：弹簧的弹力F=m2g，细绳烧断的瞬间，对于甲球有：F+m1g=m1a1，解得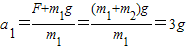
．
对于乙球，F=m2g，则a2=0．故B、C正确，A、D错误．
故选BC．
点评：解决本题的关键抓住细线烧断的瞬间，弹簧弹力不变，结合牛顿牛顿第二定律进行求解．
解答：解：弹簧的弹力F=m2g，细绳烧断的瞬间，对于甲球有：F+m1g=m1a1，解得
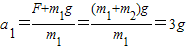．对于乙球，F=m2g，则a2=0．故B、C正确，A、D错误．
故选BC．
点评：解决本题的关键抓住细线烧断的瞬间，弹簧弹力不变，结合牛顿牛顿第二定律进行求解．
练习册系列答案
口算能手系列答案
相关题目
（2013?安徽模拟）如图所示，光滑的水平面AB与半径为R=0.32m的光滑竖直半圆轨道BCD在B点相切，D为轨道最高点．用轻质细线连接甲、乙两小球，中间夹一轻质弹簧，弹簧与甲乙两球不栓接．甲球的质量为m1=0．lkg，乙球的质量为m2=0.3kg，甲、乙两球静止在光滑的水平面上．现固定甲球，烧断细线，乙球离开弹簧后进入半圆轨道恰好能通过D点．重力加速度g取l0m/s2，甲、乙两球可看作质点．
如图2-甲所示，轻质细杆AB两端分别固定着质量均为m的小球，用两根不可伸长的轻质细线系住两球悬挂于O点，且OAB恰好为一正三角形，此时OB线的张力为F1，现对B球施加一水平拉力F，使OA保持竖直方向（如图2-乙所示），此时此时OB线的张力为F2，则与F2的关系正确的是：（）
| A．F2＞2F1 |
| B．F2＜2F1 |
| C．F2=2F1 |
| D．无法确定F2与F1的关系 |