��Ŀ����
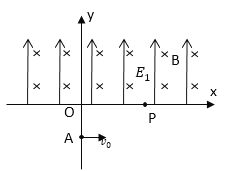
����Ŀ����ͼ��ʾ������ֱƽ���ڵ�xoyֱ������ϵ�У�x���Ϸ�������������ǿ�糡����ǿ�ų����糡ǿ��E1��������y�����ϣ��Ÿ�Ӧǿ��B������ֱֽ�����x���·����ڷ�����y�����ϵ���ǿ�糡��ͼ��δ����������ǿΪE2������Ϊm�������Ϊq�Ĵ�����С����Ϊ�ʵ㣩����y���ϵ�A�����ٶȴ�Сv0��x���������׳�����x���ϵ�P�����x�������45������x���Ϸ�ǡ��������Բ���˶���O��P��������![]() ��O��A��������
��O��A��������![]() �������¹�ϵ��
�������¹�ϵ��![]() ���������ٶ�Ϊg��������������m��q��v0��gΪ��֪������������Сδ֪��
���������ٶ�Ϊg��������������m��q��v0��gΪ��֪������������Сδ֪��
(1)�糡ǿ��E1��E2�ı�ֵ
(2)��С��ɶ�Σ��������Σ�ͨ��P�㣬��Ÿ�Ӧǿ��BΪ���
(3)��С���ǡ������ͨ��P�㣬��Ÿ�Ӧǿ��BΪ���С������ͨ��P��ʱ����Ϊ���٣�
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ��n=1��2��3����..����
��n=1��2��3����..����![]() ��n=1��2��3����..��
��n=1��2��3����..��
��������
�⣺(1)С����x���Ϸ�����Բ�ܣ��ɵã�![]()
С���A��P�Ĺ�������ƽ���˶���![]()
![]()
��ϣ�![]()
�ɵã�![]()
��ţ�ٵ������ɿɵã�![]()
��ã�![]()
�ʣ�![]()
(2) С���һ��ͨ��P��ʱ��x�������![]() ����֪С����P��ʱ���У�
����֪С����P��ʱ���У�![]()
��P��ʱ���ٶȣ�![]()
����ƽ��λ�ƹ�ʽ�ɵã�![]()
С���ξ���P�㣬�켣��ͼ����ʾ��С���ڴų����˶�![]() �����ں���x���ϵ�Q�㣬P��Q����ԭ��O�Գƣ�֮��ص�A�������ظ���һ���̣��Ӷ���ξ���P��
�����ں���x���ϵ�Q�㣬P��Q����ԭ��O�Գƣ�֮��ص�A�������ظ���һ���̣��Ӷ���ξ���P��
��С���ڴų���Բ���˶��İ뾶ΪR���ɼ��ι�ϵ�ɵã�![]()
���ɣ�![]()
������ã�![]()

(3)С��ǡ�����ξ���P�㣬�켣��ͼ����ʾ
��x���Ϸ���С���ڴų��е��˶����ڣ�![]()
��x���·���С����˶�ʱ�䣺![]()
�ɹ��ɿ�֪��С��ǡ�����ξ���P������ļ��ι�ϵΪ��![]() ��n=1��2��3����..��
��n=1��2��3����..��
��ã�![]() ��n=1��2��3����..��
��n=1��2��3����..��
����ͨ��P���ʱ����Ϊ��![]() ��n=1��2��3����..��
��n=1��2��3����..��
��ã�![]() ��n=1��2��3����..��
��n=1��2��3����..��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�