题目内容
12.如图甲、乙所示,细线均不可伸长,两小球均处于平衡状态且质量相同.如果突然把两水平细线剪断,剪断瞬间小球A的加速度的大小为gsinθ,方向为垂直于细绳向下;小球B的加速度的大小为gtanθ,方向为水平向右;剪断瞬间图甲中倾斜细线OA与图乙中弹簧的拉力之比为$co{s}_{\;}^{2}θ$(θ角已知).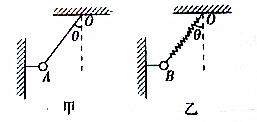
分析 剪断细线的瞬间细绳的拉力会发生突变,而弹簧的弹力不能突变,此瞬间弹力没有来得及变化.根据牛顿第二定律和平衡条件求解加速度.
解答  解:甲图中,剪断细线的瞬间,沿细绳方向的合力为零,小球的合力为 F合A=mgsinθ
解:甲图中,剪断细线的瞬间,沿细绳方向的合力为零,小球的合力为 F合A=mgsinθ
由牛顿第二定律得:${a}_{A}^{\;}=\frac{{F}_{合A}^{\;}}{m}=gsinθ$,方向垂直于细绳向下.
乙图中,剪断细线的瞬间,弹簧的弹力没有变化,小球的合力等于原来细线的拉力,为 F合B=mgtanθ
由牛顿第二定律得:${a}_{B}^{\;}=\frac{{F}_{合B}^{\;}}{m}=gtanθ$,方向水平向右.
剪断细绳瞬间图甲中倾斜细线OA的拉力:${F}_{OA}^{\;}=mgcosθ$
图乙中弹簧的拉力为:${F}_{OB}^{\;}cosθ=mg$,得${F}_{OB}^{\;}=\frac{mg}{cosθ}$
剪断瞬间图甲中倾斜细线OA与图乙中弹簧的拉力之比为$\frac{{F}_{OA}^{\;}}{{F}_{OB}^{\;}}=co{s}_{\;}^{2}θ$
故答案为:gsinθ 垂直于细绳向下;gtanθ 水平向右;$co{s}_{\;}^{2}θ$
点评 本题考查了共点力平衡和牛顿第二定律的基本运用,知道剪断细线的瞬间,弹簧的弹力不变;同时注意明确我们所求出的加速度为瞬时加速度,即为细绳剪断瞬间的加速度.

练习册系列答案
相关题目
2. 如图是质量为1kg的质点在水平面上运动的v-t图象,以水平向右的方向为正方向.以下判断正确的是( )
如图是质量为1kg的质点在水平面上运动的v-t图象,以水平向右的方向为正方向.以下判断正确的是( )
 如图是质量为1kg的质点在水平面上运动的v-t图象,以水平向右的方向为正方向.以下判断正确的是( )
如图是质量为1kg的质点在水平面上运动的v-t图象,以水平向右的方向为正方向.以下判断正确的是( )| A. | 在0~3s时间内,合力对质点做功为6J | |
| B. | 在4~6s时间内,质点的平均速度为3m/s | |
| C. | 在1~5s时间内,合力的平均功率为4W | |
| D. | 在t=6s时,质点的加速度为零 |
3.下列研究物理问题的方法相同的是( )
(a)根据磁铁产生的作用来认识磁场
(b)研究电流时把它比作水流
(c)根据电流所产生的效应认识电流
(d)利用磁感线来描述磁场.
(a)根据磁铁产生的作用来认识磁场
(b)研究电流时把它比作水流
(c)根据电流所产生的效应认识电流
(d)利用磁感线来描述磁场.
| A. | a与b | B. | a与c | C. | c与d | D. | b与d |
20.将一个弹性小球从1m高处用力竖直下抛,小球从地面弹起后,在0.5m高处被接住,则该小球在整个运动过程中( )
| A. | 位移大小是1.5m | B. | 路程是1.5m | ||
| C. | 位移大小是0.5m | D. | 位移方向是竖直向下 |
4.多快的速度才能使卫星环绕地球运行( )
| A. | 大于11.2千米/秒而小于16.4千米/秒 | |
| B. | 大于7.9千米/秒而小于11.2千米/秒 | |
| C. | 大于7.9千米/秒而小于16.4千米/秒 |
11.水平抛出一小球,t秒末速度方向与水平方向的夹角为θ1,(t+△t)秒末速度方向与水平方向的夹角为θ2,忽略空气阻力作用.则小球的初速度是( )
| A. | g△tcosθ1 | B. | g△ttanθ1 | ||
| C. | $\frac{g△t}{tan{θ}_{2}-tan{θ}_{1}}$ | D. | $\frac{g△t}{cos{θ}_{1}-cos{θ}_{2}}$ |

 甲同学设计了一道习题供乙和丙二位同学求解.乙同学和丙同学以各自的方法求解,却获得不相同的结论.显然,这不符合常识.请你通过定量分析的方法,找出其中的原因.附:
甲同学设计了一道习题供乙和丙二位同学求解.乙同学和丙同学以各自的方法求解,却获得不相同的结论.显然,这不符合常识.请你通过定量分析的方法,找出其中的原因.附: