题目内容
如图所示，在磁感应强度为B垂直纸面向里的匀强磁场中，一质量为m、带电量大小为q(电性未知)的粒子做匀速圆周运动(粒子重力不计)，在轨迹圆周上有距离为S的a、b两点，粒子通过a点时它的速度方向与ab连线成θ角(弧度)．求：
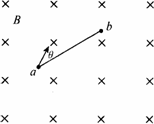
(1)粒子所带电性，画出轨迹圆心；
(2)粒子速度大小；
(3)粒子从a点运动到b点的时间．
答案：
解析：
解析：
|
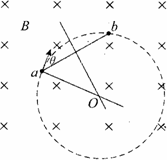
解：(1)根据左手定则可判定粒子带负电．轨迹圆圆心的确定：过a点做速度的垂线，即向心力的方向，过弦ab中点做垂线必过圆心，两线交点为轨迹圆圆心．如图所示．
(2)带电粒子做匀速圆周运动，洛仑兹力f做向心力． 根据牛顿定律 f=qBv 可得轨迹圆半径 ① 根据几何知识可知速度方向与弦ab的夹角θ为弦ab所对圆心角的一半，sinθ=S／2R，R=S／(2sinθ) ② 将②式带入①式得 (3)粒子由a点运动到b点的时间t为弦所对圆心角2θ是2π角的几分之一，t就是周期T的几分之一． 将①式带入 |
，得
，那么时间
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
如图所示，在磁感应强度为B=0.2T的匀强磁场中，导体棒AB的在金属框架上以10m/s的速度向右滑动，已知导体棒AB长为0.5m，电阻为10Ω，R1=R2=20Ω，其他电阻不计，则导体棒端点AB上的电压大小是
如图所示，在磁感应强度为B=0.2T的匀强磁场中，长为0.5m阻值为10Ω的导体棒在金属框架上以10m/s的速度向右滑动，已知R1=R2=5Ω，其他电阻不计，则导体棒两端的电压是
如图所示，在匀强磁场中有竖直放置的两平行光滑导轨，其间距L=0.5m，导轨间接有一电阻．现有一质量为m=5×10-2kg的金属棒在重力和安培力作用下，水平地沿导轨匀速下滑，此时通过电阻的电流I=2A，它们接触良好，求：
（2010?威海二模）如图所示，在磁感应强度大小为B、方向竖直向上的匀强磁场中，有一质量为m、阻值为R的闭合矩形金属线框abcd，用绝缘轻质细杆悬挂在O点，并可绕O点无摩擦摆动．金属线框从右侧某一位置由静止开始释放，细杆和金属框平面始终处于垂直纸面的同一平面内，不计空气阻力．下列判断正确的是（ ）
如图所示，在磁感应强度为B的匀强磁场中，有一矩形线框abcd，线框的匝数为N，电阻为R，ab=cd=L1，ad=bc=L2．线框绕垂直于磁感线的轴OO′以角速度ω做匀速转动．求：