题目内容
10.如图所示,在xOy平面内y>0的区域内分布着沿y轴负方向的匀强电场,在x轴下方有两个宽度相同且边界平行的条形匀强磁场区域,匀强磁场的磁感应强度大小均为B,方向垂直于xOy平面向外,磁场区域I的上边界与x轴重合,两个磁场区域的间距为l.质量为m、电荷量为q的带正电的粒子从y轴上的P点以初速度v0沿x轴正向射出,然后从x轴上的Q点射入磁场区域I.已知OP=h,OQ=$\frac{{2\sqrt{3}}}{3}h$,粒子的重力忽略不计.求
(1)粒子从x轴上的Q点射入磁场区域I时的速度大小v;
(2)若粒子未从磁场区域I的下边界穿出,求条形磁场区域的最小宽度d0;
(3)若粒子恰好没从磁场区域II的下边界穿出,求粒子从P点射入电场区域到经过两个磁场区域后返回x轴的时间t.
分析 (1)粒子从P到Q到类似平抛运动,根据分运动公式列式求解末速度的大小和方向;
(2)粒子进入磁场后做匀速圆周运动,若恰好返回,画出临界轨迹,结合几何关系求解出半径,再运用洛伦兹力提供向心力并结合牛顿第二定律列式求解;
(3)首先粒子要能够到达磁场区域Ⅲ,其次要能够从磁场区域Ⅲ返回,从而确定磁场区域Ⅲ下边界距x轴距离的范围.
解答  解:(1)粒子在电场中类平抛运动
解:(1)粒子在电场中类平抛运动
在x方向 $\frac{{2\sqrt{3}}}{3}h={v_0}t$
在y方向 $h=\frac{{0+{v_{Qy}}}}{2}t$
而$v=\sqrt{v_0^2+v_{Qy}^2}$
联立,解得v=2v0
(2)粒子在磁场区域I中匀速圆周运动 $qvB=m\frac{v^2}{r}$
恰好未从其下边界穿出,由几何关系得 rsin30°+r=d0
联立,解得${d_0}=\frac{{3m{v_0}}}{qB}$;
(3)由对称性,若把粒子在磁场中的运动衔接起来,刚好构成一个圆心角为240°的圆周,如图所示.
粒子在磁场中运动的时间为${t_1}=\frac{2}{3}T=\frac{4πm}{3qB}$
由几何关系得2d=Rsin30°+R
所以,磁场区域的宽度 $d=\frac{3}{4}R$
故有 $cosθ=\frac{{\sqrt{15}}}{4}$
粒子在无磁场区域运动的路程 $s=\frac{2l}{cosθ}$
粒子在无磁场区域运动的时间 ${t_2}=\frac{s}{v}=\frac{{4\sqrt{15}l}}{{15{v_0}}}$
粒子在电场区域运动的时间 ${t_3}=\frac{{2\sqrt{3}h}}{{3{v_0}}}$
所以,粒子从P点射入电场区域到返回x轴的时间为$t={t_1}+{t_2}+{t_3}=\frac{4πm}{3qB}+\frac{{4\sqrt{15}l}}{{15{v_0}}}+\frac{{2\sqrt{3}h}}{{3{v_0}}}$
答:(1)粒子从x轴上的Q点射入磁场区域I时的速度大小是2v0;
(2)若粒子未从磁场区域I的下边界穿出,条形磁场区域的最小宽度是$\frac{3m{v}_{0}}{qB}$;
(3)若粒子恰好没从磁场区域II的下边界穿出,粒子从P点射入电场区域到经过两个磁场区域后返回x轴的时间是$\frac{4πm}{3qB}+\frac{4\sqrt{15}l}{15{v}_{0}}+\frac{2\sqrt{3}h}{3{v}_{0}}$.
点评 本题第一问关键明确粒子现在类似平抛运动,然后做匀速圆周运动,关键是画出磁场中的临界轨迹;第三问磁场中的轨迹可以合成同一个圆周.

| A. |  分子并不是球形,但可以把它们当做球形处理,是一种估算方法 | |
| B. |  微粒运动就是物质分子的无规则热运动,即布朗运动 | |
| C. |  当两个相邻的分子间距离为r0时,它们间相互作用的引力和斥力大小相等 | |
| D. |  实验中尽可能保证每一粒玻璃珠与秤盘碰前的速度相同 | |
| E. | 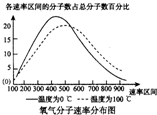 0℃和100℃氧气分子速率都呈现“中间多两头少”的分布特点 |
 已知质量分布均匀的球壳对壳内物体的引力为零.假设月球是半径为R、质量分布均匀的球体,距离月心为r处的重力加速度g与r的关系如图所示.已知引力常量为G,月球表面的重力加速度大小为g0,由上述信息可知( )
已知质量分布均匀的球壳对壳内物体的引力为零.假设月球是半径为R、质量分布均匀的球体,距离月心为r处的重力加速度g与r的关系如图所示.已知引力常量为G,月球表面的重力加速度大小为g0,由上述信息可知( )| A. | 距离月心$\frac{R}{2}$处的重力加速度为$\frac{g_0}{4}$ | B. | 距离月心2R处的重力加速度为$\frac{g_0}{4}$ | ||
| C. | 月球的质量为$\frac{{{g_0}{R^2}}}{G}$ | D. | 月球的平均密度为$\frac{{3{g_0}}}{4πG}$ |
 如图所示,一束复色光a由空气中斜射到上下表面平行的厚平板玻璃的上表面,穿过玻璃后分为b、c两束平行单色光从下表面射出.关于这两束单色光,下列说法正确的是( )
如图所示,一束复色光a由空气中斜射到上下表面平行的厚平板玻璃的上表面,穿过玻璃后分为b、c两束平行单色光从下表面射出.关于这两束单色光,下列说法正确的是( )| A. | 此玻璃对b光的折射率等于对c光的折射率 | |
| B. | 在真空中b光的传播速度等于c光的传播速度 | |
| C. | 在此玻璃中b光的全反射临界角大于c光的全反射临界角 | |
| D. | 用同一双缝干涉装置进行实验,屏上b光相邻的干涉条纹间距比c光的宽 |
 如图,同一水平面上足够长的固定平行导轨MN、PQ位于垂直于纸面向里的匀强磁场中,导轨上有两根金属棒ab、cd,都能沿导轨无摩擦滑动,金属棒和导轨间接触良好,开始ab、cd都静止.现给cd一个向右的初速度v0,则下列说法中正确的是( )
如图,同一水平面上足够长的固定平行导轨MN、PQ位于垂直于纸面向里的匀强磁场中,导轨上有两根金属棒ab、cd,都能沿导轨无摩擦滑动,金属棒和导轨间接触良好,开始ab、cd都静止.现给cd一个向右的初速度v0,则下列说法中正确的是( )| A. | cd先做减速运动后做匀速运动 | B. | 运动中有可能追上cd | ||
| C. | ab先做加速运动后做匀速运动 | D. | 最终两杆以相同的速度做匀速运动 |
| A. | 6cm | B. | 3cm | C. | 1.5cm | D. | 0.75cm |
 水平放置的两块平金属板长L,两板间距d,两板间电压为U,且上板为正,一个电子沿水平方向以速度v0,从两板中间射入,如图所示,已知电子质量为m,电量为e,求:(电子的重力不计)
水平放置的两块平金属板长L,两板间距d,两板间电压为U,且上板为正,一个电子沿水平方向以速度v0,从两板中间射入,如图所示,已知电子质量为m,电量为e,求:(电子的重力不计) 如图所示,劲度系数k0=2N/m、自然长度l0=$\sqrt{2}$m的轻弹簧两端分别连接着带正电的小球A和B,A、B的电荷量分别为qA=4.0×10-2C、qB=1.0×10-8C,B的质量m=0.18kg,A球固定在天花板下0点,B球套在与0点等高的光滑固定直杆的顶端,直杆长L=2$\sqrt{2}$m、与水平面的夹角θ=45°,直杆下端与一圆心在O点、半径R=2m、长度可忽略的小圆弧杆CO′D平滑对接,O′O为竖直线,O′的切线为水平方向,整个装置处于同一竖直面内.若小球A、B均可视为点电荷,且A、B与天花板、弹簧、杆均绝缘,重力加速度g=10m/s2,静电力常量k=9.0×109 N•m2/C2,则将B球从直杆顶端无初速释放后,求:
如图所示,劲度系数k0=2N/m、自然长度l0=$\sqrt{2}$m的轻弹簧两端分别连接着带正电的小球A和B,A、B的电荷量分别为qA=4.0×10-2C、qB=1.0×10-8C,B的质量m=0.18kg,A球固定在天花板下0点,B球套在与0点等高的光滑固定直杆的顶端,直杆长L=2$\sqrt{2}$m、与水平面的夹角θ=45°,直杆下端与一圆心在O点、半径R=2m、长度可忽略的小圆弧杆CO′D平滑对接,O′O为竖直线,O′的切线为水平方向,整个装置处于同一竖直面内.若小球A、B均可视为点电荷,且A、B与天花板、弹簧、杆均绝缘,重力加速度g=10m/s2,静电力常量k=9.0×109 N•m2/C2,则将B球从直杆顶端无初速释放后,求: