题目内容
16. 为了解释光电效应现象,爱因斯坦提出了“光子”的概念,并给出了光电效应方程.但这一观点一度受到质疑,密立根通过下述实验来验证其理论的正确性,实验电路如图1所示.
为了解释光电效应现象,爱因斯坦提出了“光子”的概念,并给出了光电效应方程.但这一观点一度受到质疑,密立根通过下述实验来验证其理论的正确性,实验电路如图1所示.(1)为了测量遏止电压U0 与入射光频率的关系,实验中双刀双掷开关应向下闭合.(填“上”或“下”)
(2)如果实验所得U0-v图象如图2所示,其中U1、v1、v0为已知量,元电荷带电量为e,那么:
①只需将$\frac{e{U}_{1}}{{v}_{1}-{v}_{0}}$与普朗克常量h进行比较,若在误差许可的范围内二者相等,则证明“光电效应方程”是正确的.
②该实验所用光电管的K极材料的逸出功为$\frac{e{U}_{1}}{{v}_{1}-{v}_{0}}•{v}_{0}$.
分析 (1)测量遏止电压需要将阴极K接电源的正极,由此判断即可.
(2)根据光电效应方程得出遏止电压与入射光频率的关系,通过图线的斜率求出普朗克常量.遏止电压为零时,入射光的频率等于截止频率.
解答 解:(1)测量遏止电压需要将阴极K接电源的正极,可知实验中双刀双掷开关应向 下闭合.
(2)①根据爱因斯坦光电效应方程:
Ek=hv-W0
由动能定理:eU=Ek得:
U1=$\frac{h}{e}$v1-$\frac{h}{e}$v0,
结合图象知:k=$\frac{h}{e}$=$\frac{{U}_{1}}{{v}_{1}-{v}_{0}}$;
解得,普朗克常量:h=$\frac{e{U}_{1}}{{v}_{1}-{v}_{0}}$,
②截止频率为v0,则该金属的逸出功:W0=hv0=$\frac{e{U}_{1}}{{v}_{1}-{v}_{0}}•{v}_{0}$;
故答案为:(1)下;(2)①$\frac{e{U}_{1}}{{v}_{1}-{v}_{0}}$;②$\frac{e{U}_{1}}{{v}_{1}-{v}_{0}}•{v}_{0}$.
点评 解决本题的关键掌握光电效应方程,对于图象问题,关键得出物理量之间的关系式,结合图线的斜率或截距进行求解,解决本题的关键掌握光电效应方程以及最大初动能与遏止电压的关系.

练习册系列答案
相关题目
2. 图甲是某质点的位移一时间图象,图乙是另一质点的速度一时间图象,关于这两个图象,下列方法正确的是( )
图甲是某质点的位移一时间图象,图乙是另一质点的速度一时间图象,关于这两个图象,下列方法正确的是( )
 图甲是某质点的位移一时间图象,图乙是另一质点的速度一时间图象,关于这两个图象,下列方法正确的是( )
图甲是某质点的位移一时间图象,图乙是另一质点的速度一时间图象,关于这两个图象,下列方法正确的是( )| A. | 由图乙可知,质点在第4s内加速度的方向与物体运动的方向相反 | |
| B. | 由图甲可知,质点做曲线运动,且速度逐渐增大 | |
| C. | 由图乙可知,质点在运动过程中,加速度的最大值为15m/s2 | |
| D. | 由图甲可知,质点在前10s内的平均速度的大小为2m/s |
4.若人造卫星绕地球做匀速圆周运动,则离地面越近的卫星( )
| A. | 速度越大 | B. | 角速度越大 | C. | 向心加速度越大 | D. | 周期越长 |
11.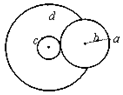 如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )
如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )
 如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )
如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )| A. | b点与d点的线速度大小相等 | |
| B. | a点与c点的线速度大小相等 | |
| C. | c点与b点的角速度大小不相等 | |
| D. | a点与d点的向心加速度大小之比为1:8 |
1.关于曲线运动,以下说法正确的是( )
| A. | 做曲线运动的物体一定受力,且力必须是恒力 | |
| B. | 曲线运动不一定是变速运动 | |
| C. | 匀速圆周运动是一种线速度不断改变的运动 | |
| D. | 做圆周运动的物体加速度一定指向圆心 |
5. 如图所示,细绳一端系着质量为M=0.6kg的物体,静止在水平面上,另一端通过光滑小孔O吊着质量m=0.3kg的物体,M与圆孔距离为0.2m,已知M和水平面的最大静摩擦力为2N.现使此平面绕中心轴转动,为使M与盘面不出现相对滑动,盘面转动的角速度可以为:(取g=10m/s2)( )
如图所示,细绳一端系着质量为M=0.6kg的物体,静止在水平面上,另一端通过光滑小孔O吊着质量m=0.3kg的物体,M与圆孔距离为0.2m,已知M和水平面的最大静摩擦力为2N.现使此平面绕中心轴转动,为使M与盘面不出现相对滑动,盘面转动的角速度可以为:(取g=10m/s2)( )
 如图所示,细绳一端系着质量为M=0.6kg的物体,静止在水平面上,另一端通过光滑小孔O吊着质量m=0.3kg的物体,M与圆孔距离为0.2m,已知M和水平面的最大静摩擦力为2N.现使此平面绕中心轴转动,为使M与盘面不出现相对滑动,盘面转动的角速度可以为:(取g=10m/s2)( )
如图所示,细绳一端系着质量为M=0.6kg的物体,静止在水平面上,另一端通过光滑小孔O吊着质量m=0.3kg的物体,M与圆孔距离为0.2m,已知M和水平面的最大静摩擦力为2N.现使此平面绕中心轴转动,为使M与盘面不出现相对滑动,盘面转动的角速度可以为:(取g=10m/s2)( )| A. | 2.0rad/s | B. | 3.14 rad/s | C. | 6.0 rad/s | D. | 7.9 rad/s |

 如图所示为固定在竖直平面内的轨道,直轨道AB与光滑圆弧轨道 BC相切,圆弧轨道的圆心角为37°,半径r=0.25m,C端水平,AB段的动摩擦因数为0.5.竖直墙壁CD高H=0.2m,紧靠墙壁在地面上固定一个和CD等高、底边长L=0.3m的斜面.一个质量m=0.1kg 的小物块(视为质点)在倾斜轨道上从距离B点l=0.5m处由静止释放,从C点水平抛出.重力加速度g=10m/s2,sin 37°=0.6,cos 37°=0.8.求:
如图所示为固定在竖直平面内的轨道,直轨道AB与光滑圆弧轨道 BC相切,圆弧轨道的圆心角为37°,半径r=0.25m,C端水平,AB段的动摩擦因数为0.5.竖直墙壁CD高H=0.2m,紧靠墙壁在地面上固定一个和CD等高、底边长L=0.3m的斜面.一个质量m=0.1kg 的小物块(视为质点)在倾斜轨道上从距离B点l=0.5m处由静止释放,从C点水平抛出.重力加速度g=10m/s2,sin 37°=0.6,cos 37°=0.8.求: