题目内容
10. 如图所示,坐标系xoy在光滑水平面内,磁场方向竖直向下,磁感应强度B的大小与坐标x的关系为B=kx(k为常亮),在水平面内,一质量为m、边长为L的正方形线框的电阻为R,其左边与y轴重合,线框在沿x轴正方向拉力作用下从静止开始运动,拉力的功率始终为P,若线框从静止开始到匀速运动的过程中,产生的焦耳热为Q,求此过程所用的时间.
如图所示,坐标系xoy在光滑水平面内,磁场方向竖直向下,磁感应强度B的大小与坐标x的关系为B=kx(k为常亮),在水平面内,一质量为m、边长为L的正方形线框的电阻为R,其左边与y轴重合,线框在沿x轴正方向拉力作用下从静止开始运动,拉力的功率始终为P,若线框从静止开始到匀速运动的过程中,产生的焦耳热为Q,求此过程所用的时间.
分析 线框在运动过程中,有法拉第电磁感应定律分别求得,左右两边产生的电动势E1E2,再由右手定则确定电流方向,求出回路中电流大小I,根据动能定理结合功、功率知识点求解运动时间.
解答 解:设线框向右运动x时,开始匀速运动,右边产生的电动势:E2=B2Lv,而B2=k(x+L),同理,左边E1=B1Lv,而B1=Kx,
由右手定则可知,右左两边中感应电流方向均向上,故整个回路中感应电流,$I=\frac{{E}_{2}-{E}_{1}}{R}=\frac{k(x+L)Lv-kxLv}{R}=\frac{k{L}^{2}v}{R}$,
线圈做匀速运动,则线框受力平衡即:F=F安----①,
有左手定则得:${F}_{安}{=B}_{2}IL-{B}_{1}IL=k{L}^{2}I=\frac{{k}^{2}{L}^{4}v}{R}$----②,
联立①②两式解得:$F=\frac{{k}^{2}{L}^{4}}{R}v$,又有:P=Fv,得:${v}^{2}=\frac{PR}{{k}^{2}{L}^{4}}$,
线框从静止开始到匀速运动的过程,由动能定理得:$Pt-Q=\frac{1}{2}m{v}^{2}$,解得:t=$\frac{mR}{2{k}^{2}{L}^{4}}+\frac{Q}{P}$,
答:线框从静止开始到匀速运动所用的时间为$\frac{mR}{2{k}^{2}{L}^{4}}+\frac{Q}{P}$.
点评 本题用到的知识有动能定理,法拉第电磁感应定律,欧姆定律等基本知识点,但本题关键在于回路中感应电流大小计算和利用功和功率计算时间.

练习册系列答案
相关题目
20.如图,A、B是相同的白炽灯,L是自感系数很大,电阻可忽略的自感线圈.下面说法正确的是( )


| A. | 闭合开关S时,A、B灯同时亮,且达到正常 | |
| B. | 闭合开关S时,B灯比A灯先亮,最后一样亮 | |
| C. | 闭合开关S时,A灯比B灯先亮,最后A比B亮 | |
| D. | 断开开关S时,A灯与B灯同时逐渐熄灭 |
1.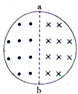 如图所示,在图形空间区域内存在关于直径ab对称、方向相反的两个匀强磁场,两磁场的磁感应强度大小相等,一金属导线制成的圆环刚好与磁场边界重合,下列说法错误的是( )
如图所示,在图形空间区域内存在关于直径ab对称、方向相反的两个匀强磁场,两磁场的磁感应强度大小相等,一金属导线制成的圆环刚好与磁场边界重合,下列说法错误的是( )
 如图所示,在图形空间区域内存在关于直径ab对称、方向相反的两个匀强磁场,两磁场的磁感应强度大小相等,一金属导线制成的圆环刚好与磁场边界重合,下列说法错误的是( )
如图所示,在图形空间区域内存在关于直径ab对称、方向相反的两个匀强磁场,两磁场的磁感应强度大小相等,一金属导线制成的圆环刚好与磁场边界重合,下列说法错误的是( )| A. | 若使圆环向右平动,感应电流先沿逆时针方向后沿顺时针方向 | |
| B. | 若使圆环竖直向上平动,则圆环中无感应电流 | |
| C. | 若圆环以ab为轴转动,a点的电势一定高于b点的电势 | |
| D. | 若圆环以ab为轴转动,b点的电势一定高于a点的电势 |
2. 通过挂有动滑轮的绳子,两端分别系于天花板上A、B两点,如图所示.把B点缓慢靠近A点的过程中,绳子上的拉力( )
通过挂有动滑轮的绳子,两端分别系于天花板上A、B两点,如图所示.把B点缓慢靠近A点的过程中,绳子上的拉力( )
 通过挂有动滑轮的绳子,两端分别系于天花板上A、B两点,如图所示.把B点缓慢靠近A点的过程中,绳子上的拉力( )
通过挂有动滑轮的绳子,两端分别系于天花板上A、B两点,如图所示.把B点缓慢靠近A点的过程中,绳子上的拉力( )| A. | 变小 | B. | 变大 | C. | 先变大,后变小 | D. | 先变小,后变大 |
19.变频空调是与传统的定频空调相比较而产生的概念,我国日常生活所用的交流电为220v,50Hz,在这种条件下工作的空调称为“定频空调”由于供电频率不能改变,传统的定频空调的压缩机转速基本不变,变频空调中的变频器可以改变压缩机的供电频率,把50Hz的固定电网频率变为30至130Hz的变化频率,从而调节压缩机转速,空调节能省电,下列说法正确的( )
| A. | 供电频率高,压缩机转速大,空调器的制冷量大 | |
| B. | 供电频率低,压缩机转速小,空调器的制冷量大 | |
| C. | 变频空调只能改变压缩机的供电频率,不能改变电网的交流电频率 | |
| D. | 变频空调既能改变压缩机的供电频率,又能改变电网的交流电频率 |
14.下列各项物理量中全部是矢量的是( )
| A. | 位移、力、电荷量、速度 | B. | 重力、路程、时间、速度 | ||
| C. | 密度、时间、质量、路程 | D. | 浮力、加速度、位移、摩擦力 |
 如图所示,用滑轮组拉着重物在水平地面上匀速前进,作用在绳的端点A的力F=300N,滑轮组的机械效率为80%,问重物与地面间的摩擦力f为多大?
如图所示,用滑轮组拉着重物在水平地面上匀速前进,作用在绳的端点A的力F=300N,滑轮组的机械效率为80%,问重物与地面间的摩擦力f为多大?