题目内容
 如图甲所示,真空中的电极K连续不断地发出电子(电子的初速度可忽略不计),经电压为u的电场加速,加速电压u随时间t变化的图象如图乙所示.每个电子通过加速电场的过程时间极短,可认为加速电压不变.电子被加速后由小孔S穿出,沿两个彼此靠近且正对的水平金属板A、B间中轴线从左边缘射入A、B两板间的偏转电场,A、B两板长均为L=0.20m,两板之间距离d=0.050m,A板的电势比B板的电势高.A、B板右侧边缘到竖直放置的荧光屏P(面积足够大)之间的距离b=0.10m.荧光屏的中心点O与A、B板的中心轴线在同一水平直线上.不计电子之间的相互作用力及其所受的重力,求:
如图甲所示,真空中的电极K连续不断地发出电子(电子的初速度可忽略不计),经电压为u的电场加速,加速电压u随时间t变化的图象如图乙所示.每个电子通过加速电场的过程时间极短,可认为加速电压不变.电子被加速后由小孔S穿出,沿两个彼此靠近且正对的水平金属板A、B间中轴线从左边缘射入A、B两板间的偏转电场,A、B两板长均为L=0.20m,两板之间距离d=0.050m,A板的电势比B板的电势高.A、B板右侧边缘到竖直放置的荧光屏P(面积足够大)之间的距离b=0.10m.荧光屏的中心点O与A、B板的中心轴线在同一水平直线上.不计电子之间的相互作用力及其所受的重力,求:(1)要使电子都打不到荧光屏上,则A、B两板间所加电压U应满足什么条件;
(2)当A、B板间所加电压U'=50V时,电子打在荧光屏上距离中心点O多远的范围内.
分析:(1)电子在加速中,由动能定理求出获得的速度.在偏转电场中,电子做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,由牛顿第二定律和运动学公式结合可得到偏转距离与偏转电压等的关系式,要使电子都打不到荧光屏上,偏转距离大于等于
,即可求出U满足的条件;
(2)当A、B板间所加电压U′=50V时,先求出电子通过偏转电场时偏转的距离,根据三角形相似法求解电子打在荧光屏上的距离.
| d |
| 2 |
(2)当A、B板间所加电压U′=50V时,先求出电子通过偏转电场时偏转的距离,根据三角形相似法求解电子打在荧光屏上的距离.
解答:解:电子加速过程中,根据动能定理有:
eU1=
mv2
偏转过程中,由牛顿第二定律有:eE=ma
而 E=
,L=vt,y=
at2
有 y=
?
?(
)2=
要使电子都打不到屏上,应满足U1取最大值800V时仍有y>0.5d
代入上式可得,U2=
>
=
V=100V
所以为使电子都打不到屏上,A、B两板间所加电压U2至少为100V.
(2)当A、B板间所加电压U′=50V时,代入
当电子恰好从A板右边缘射出偏转电场时,
其侧移最大ymax=
d=
×0.05m=0.025m.
设电子通过电场最大的偏转角为θ,设电子打在屏上距中心点的最大距离为Ymax,则:
tanθ=
=
Ymax=ymax+
vy=ymax+
又ymax=
t,vt=L
得vyt=2ymax,联立得Ymax=ymax+
ymax=0.025+
×0.025=0.05m
由第(1)问中的y=
可知,在其它条件不变的情况下,U1越大y越小,
所以当U1=800V时,电子通过偏转电场的侧移量最小,
其最小侧移量,ymin=
=
=
m=0.0125m
同理,电子打在屏上距中心的最小距离 Ymin=ymin+
ymin=0.0125+
×0.125=0.025m
所以电子打在屏上距中心点O在0.025m~0.05m范围内.
答:
(l)要使电子都打不到荧光屏上,则A,B两板间所加电压U应满足至少为100V条件;
(2)当A、B板间所加电U′=50V时,打到荧光屏上的电子距离中心点O在0.025m~0.05m的范围内.
eU1=
| 1 |
| 2 |
偏转过程中,由牛顿第二定律有:eE=ma
而 E=
| U2 |
| d |
| 1 |
| 2 |
有 y=
| 1 |
| 2 |
| eU2 |
| md |
| L |
| v |
| U2L2 |
| 4U1d |
要使电子都打不到屏上,应满足U1取最大值800V时仍有y>0.5d
代入上式可得,U2=
| 4U1dy |
| L2 |
| 4U1d?0.5d |
| L2 |
| 4×800×0.5×0.052 |
| 0.22 |
所以为使电子都打不到屏上,A、B两板间所加电压U2至少为100V.
(2)当A、B板间所加电压U′=50V时,代入
当电子恰好从A板右边缘射出偏转电场时,
其侧移最大ymax=
| 1 |
| 2 |
| 1 |
| 2 |
设电子通过电场最大的偏转角为θ,设电子打在屏上距中心点的最大距离为Ymax,则:
tanθ=
| vy |
| v2 |
| at |
| v |
Ymax=ymax+
| b |
| v |
| bvyt |
| vt |
又ymax=
| 0+vy |
| 2 |
得vyt=2ymax,联立得Ymax=ymax+
| 2b |
| L |
| 2×0.1 |
| 0.2 |
由第(1)问中的y=
| U2L2 |
| 4U1d |
所以当U1=800V时,电子通过偏转电场的侧移量最小,
其最小侧移量,ymin=
| U2L2 |
| 4U1d |
| U′L2 |
| 4U1d |
| 50×0.22 |
| 4×800×0.05 |
同理,电子打在屏上距中心的最小距离 Ymin=ymin+
| 2b |
| L |
| 2×0.1 |
| 0.2 |
所以电子打在屏上距中心点O在0.025m~0.05m范围内.
答:
(l)要使电子都打不到荧光屏上,则A,B两板间所加电压U应满足至少为100V条件;
(2)当A、B板间所加电U′=50V时,打到荧光屏上的电子距离中心点O在0.025m~0.05m的范围内.
点评:考查电子在电场中做类平抛运动,学会运动的分解,并根据运动学公式与牛顿第二定律及动能定理综合解题,强调电子在不同的电场中的运动与受力情况.本题的关键是确定临界条件,运用几何知识求解电子打在荧光屏上的位置.

练习册系列答案
相关题目

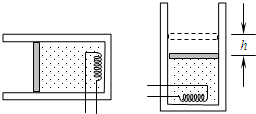 [选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
[选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.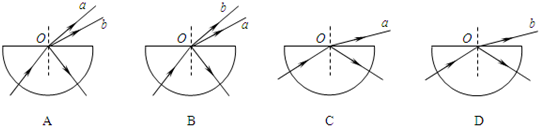
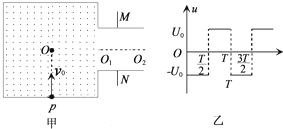 如图甲所示,在真空中,有一边长为a的正方形区域内存在匀强磁场,磁场方向垂直纸面向外.在磁场右侧有一对平行金属板M和N,两板间距及板长均为b,板间的中心线O1O2与正方形的中心O在同一直线上.有一电荷量为q、质量为m的带正电的粒子以速度v0从正方形的底边中点P沿PO方向进入磁场,从正方形右侧O1点水平飞出磁场时,立即给M、N两板加上如图乙所示的交变电压,最后粒子刚好以平行于M板的速度从M板的边缘飞出.(不计粒子所受到的重力、两板正对面之间为匀强电场,边缘电场不计)
如图甲所示,在真空中,有一边长为a的正方形区域内存在匀强磁场,磁场方向垂直纸面向外.在磁场右侧有一对平行金属板M和N,两板间距及板长均为b,板间的中心线O1O2与正方形的中心O在同一直线上.有一电荷量为q、质量为m的带正电的粒子以速度v0从正方形的底边中点P沿PO方向进入磁场,从正方形右侧O1点水平飞出磁场时,立即给M、N两板加上如图乙所示的交变电压,最后粒子刚好以平行于M板的速度从M板的边缘飞出.(不计粒子所受到的重力、两板正对面之间为匀强电场,边缘电场不计) 
