题目内容
一个质量为m，电量为+q的小球套在绝缘长杆上，球与杆间的动摩擦因数为μ，整个装置放在匀强电场与匀强磁场互相垂直的复合场中，如图所示．若已知电场强度为E，磁感应强度为B，由静止开始释放小球，求：（1）当杆对球的支持力为零时，小球的速度和加速度各为多大？
（2 ） 小球加速度多大时，速度最大？最大速度是多少？
分析：先对小球进行受力分析，结合洛伦兹力的公式求小球的速度，然后根据牛顿第二定律求加速度；
当小球受力平衡时速度最大．
当小球受力平衡时速度最大．
解答：解：（1）当杆对球的支持力为零时有：
qvB=mg
小球的速度为：v=
小球的加速度为：a=
（2 ） 小球加速度a=0时，速度最大，此时有：
qE=μ（qVmB-mg）
最大速度为：Vm=
答：（1）当杆对球的支持力为零时，小球的速度为
，加速度为
．
（2 ） 小球加速度为0时时，速度最大，最大速度是度为
．
qvB=mg
小球的速度为：v=| mg |
| qB |
小球的加速度为：a=
| qE |
| m |
（2 ） 小球加速度a=0时，速度最大，此时有：
qE=μ（qVmB-mg）
最大速度为：Vm=
(mg+
| ||
| Bq |
答：（1）当杆对球的支持力为零时，小球的速度为
| mg |
| qB |
| qE |
| m |
（2 ） 小球加速度为0时时，速度最大，最大速度是度为
(mg+
| ||
| Bq |
点评：考查如何对物体受力分析，理解牛顿第二定律的应用，抓住滑动摩擦力等于零时，加速度最大．而合力为零时，速度最大．注意洛伦兹力与速度的存在紧密联系．
练习册系列答案
小学课时特训系列答案
相关题目
如图所示，水平方向的匀强电场的场强为E，电场区宽度为L，竖直方向足够长，紧挨着电场的是垂直纸面向外的两个匀强磁场区域，其磁感应强度分别为B和2B．一个质量为m、电量为q的带正电的粒子（不计重力）从电场的边界MN上的a点由静止释放，经电场加速后进入磁场，经过tB=πm/4qB 时间穿过中间磁场，进入右边磁场，然后按某一路径再返回到电场的边界MN上的某一点b（虚线为场区的分界面），求：
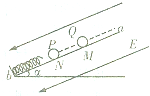如图所示，倾角为a的光滑斜面下端固定一绝缘轻弹簧，M点固定一个质量为m、带电量为-q的小球Q，整个装置处在电场强度大小为E、方向沿斜面向下的匀强电场中．现把一个带电量为+q的小球P从N点由静止释放，释放后P沿着斜面向下运动，N点与弹簧的上端和M的距离均为s0，P、Q以及弹簧的轴线ab与斜面平行，两小球均可视为质点和点电荷，弹簧的劲度系数为k0，静电力常量为k．则（ ）| A、小球P返回时，可能撞到小球Q | ||||
B、小球P在N点的加速度大小为
| ||||
| C、小球P沿着斜面向下运动过程中，其电势能可能增大 | ||||
D、当弹簧的压缩量为
|
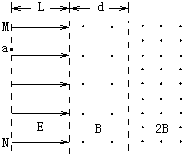如图所示，水平方向的匀强电场的场强为E，场区宽度为L，竖直方向足够长．紧挨着电场的是垂直于纸面向外的两个匀强磁场区域，其磁感应强度分别为B和2B．一个质量为m，电量为q的带正电粒子，其重力不计，从电场的边界MN上的a点由静止释放，经电场加速后进入磁场，经过时间tB＝
穿过中间磁场，进入右边磁场后能按某一路径再返回到电场的边界MN上的某一点b，途中虚线为场区的分界面．求：
，进入右边磁场后能按某一路径再返回到电场的边界MN上的某一点b，途中虚线为场区的分界面。求：
，进入右边磁场后能按某一路径再返回到电场的边界MN上的某一点b，途中虚线为场区的分界面。求：