题目内容
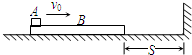 如图所示,木板B的质量M=2kg,与右墙距离为S.物体A(可视为质点)质量m=1g,以初速度v0=6m/s从左端水平滑上B.己知A与B间的动摩擦因数μ=0.2,在B第一次撞墙前,A已经与B相对静止.地面光滑,B与两面墙的碰撞都是弹性的.求:
如图所示,木板B的质量M=2kg,与右墙距离为S.物体A(可视为质点)质量m=1g,以初速度v0=6m/s从左端水平滑上B.己知A与B间的动摩擦因数μ=0.2,在B第一次撞墙前,A已经与B相对静止.地面光滑,B与两面墙的碰撞都是弹性的.求:①S的最小值;
②若A始终未滑离B,A相对于B滑行的总路程是多少?
分析:1、A在B上滑动至AB速度相等的过程中,以AB组成的系统满足动量守恒,列出等式求出共同速度,再运到动能定理求解.
2、经过足够多次的碰撞后,由于不断有摩擦力做功,最终AB速度都变为零,根据能量守恒列出等式求解.
2、经过足够多次的碰撞后,由于不断有摩擦力做功,最终AB速度都变为零,根据能量守恒列出等式求解.
解答:解:①设B与挡板相碰时的速度大小为v1,A在B上滑动至AB速度相等的过程中,规定向右为正方向,
以AB组成的系统满足动量守恒得:
mv0=(M+m)v1,
解得:v1=2m/s.
A与B刚好共速时B到达挡板S距离最短,对B用动能定理,有:
μmgS=
Mv2
S的最小值为:S=2m
②经过足够多次的碰撞后,由于不断有摩擦力做功,最终A、B速度都变为零,
则在整个过程中,平板车和物块的动能都克服摩擦力做功转化为内能,根据能量守恒因此有:
μmgx=
mv02
解得:x=9m
答:①S的最小值是2m;
②若A始终未滑离B,A相对于B滑行的总路程是9m.
以AB组成的系统满足动量守恒得:
mv0=(M+m)v1,
解得:v1=2m/s.
A与B刚好共速时B到达挡板S距离最短,对B用动能定理,有:
μmgS=
| 1 |
| 2 |
S的最小值为:S=2m
②经过足够多次的碰撞后,由于不断有摩擦力做功,最终A、B速度都变为零,
则在整个过程中,平板车和物块的动能都克服摩擦力做功转化为内能,根据能量守恒因此有:
μmgx=
| 1 |
| 2 |
解得:x=9m
答:①S的最小值是2m;
②若A始终未滑离B,A相对于B滑行的总路程是9m.
点评:解决本题的关键是A与B组成的系统在碰撞过程中满足动量守恒和能量守恒,知道摩擦力与路程的乘积等于系统机械能的损耗.

练习册系列答案
相关题目
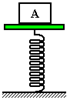 如图所示,木板固定在劲度系数为k的轻质弹簧上,弹簧与地面连在一起.现把质量为m的木块A放在木板上,并用力将木块A向下压,然后突然放手,木块A随即被弹射出去,则在木块A脱离木板之前,木块A的运动情况为( )
如图所示,木板固定在劲度系数为k的轻质弹簧上,弹簧与地面连在一起.现把质量为m的木块A放在木板上,并用力将木块A向下压,然后突然放手,木块A随即被弹射出去,则在木块A脱离木板之前,木块A的运动情况为( ) 如图所示,在光滑的水平桌面上有一质量mC=5kg的长木板C,它的两端各有一块挡板.在板的正中央并排放着两个滑块A和B,它们的质量分别为mA=1kg,mB=4kg.A、B间有一个被压缩的轻质弹簧.开始时A、B、C均处于静止,突然松开弹簧,在极短的时间内弹簧将A、B弹出,A以vA=6m/s的速率水平向左滑动.两滑块与挡板碰后都与挡板结成一体,且与挡板碰撞时间极短.不计A、B和C间的摩擦.
如图所示,在光滑的水平桌面上有一质量mC=5kg的长木板C,它的两端各有一块挡板.在板的正中央并排放着两个滑块A和B,它们的质量分别为mA=1kg,mB=4kg.A、B间有一个被压缩的轻质弹簧.开始时A、B、C均处于静止,突然松开弹簧,在极短的时间内弹簧将A、B弹出,A以vA=6m/s的速率水平向左滑动.两滑块与挡板碰后都与挡板结成一体,且与挡板碰撞时间极短.不计A、B和C间的摩擦.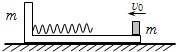 如图所示,在光滑的水平面上有质量相等的木块A和木板B,木块A以速度v0向左滑上静止的木板B的水平上表面,木板B上表面光滑,木板左端固定一轻质弹簧.当木块A碰到木板B左侧的弹簧至压缩的过程中,下列判断正确的是( )
如图所示,在光滑的水平面上有质量相等的木块A和木板B,木块A以速度v0向左滑上静止的木板B的水平上表面,木板B上表面光滑,木板左端固定一轻质弹簧.当木块A碰到木板B左侧的弹簧至压缩的过程中,下列判断正确的是( )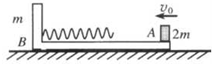
 一斜面固定在水平面上,在斜面顶端有一长木板,木板与斜面之间的动摩擦因数为?,木板上固定一轻质弹簧测力计,弹簧测力计下面固定一个光滑的小球如图所示,木板固定时,弹簧测力计示数为F1,由静止释放后木板沿斜面下滑,稳定时弹簧测力计的示数为F2,斜面的高为h,底边长为d,则下列说法正确的是( )
一斜面固定在水平面上,在斜面顶端有一长木板,木板与斜面之间的动摩擦因数为?,木板上固定一轻质弹簧测力计,弹簧测力计下面固定一个光滑的小球如图所示,木板固定时,弹簧测力计示数为F1,由静止释放后木板沿斜面下滑,稳定时弹簧测力计的示数为F2,斜面的高为h,底边长为d,则下列说法正确的是( )