题目内容
如图所示，两个单摆A和B的摆长LA＞LB，将它们都拉离竖直方向一个很小的角度θ然后释放，那么这两个摆球到达最低点时的速度υ的大小和经历时间t应满足（ ）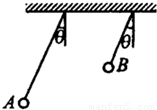
A．υA＞υB，tA＞tB
B．υA＞υB，tA＜tB
C．υA＜υB，tA＜tB
D．υA＜υB，tA＞tB
【答案】分析：单摆的小角度摆动是简谐运动，根据周期公式比较时间；根据机械能守恒定律比较最低点速度．
解答：解：单摆的小角度摆动是简谐运动，根据周期公式T=2π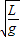
，摆长越长，周期越长，故tA＞tB；
根据机械能守恒定律，有：mgl（1-cosθ）=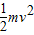
，解得：v=
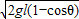，摆长越长，最低点速度越大，故υA＞υB；
故选A．
点评：本题需明确两点：单摆的小角度摆动是简谐运动，摆动过程中机械能守恒．
解答：解：单摆的小角度摆动是简谐运动，根据周期公式T=2π
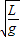，摆长越长，周期越长，故tA＞tB；根据机械能守恒定律，有：mgl（1-cosθ）=
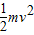，解得：v=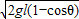，摆长越长，最低点速度越大，故υA＞υB；故选A．
点评：本题需明确两点：单摆的小角度摆动是简谐运动，摆动过程中机械能守恒．
练习册系列答案
相关题目
如图所示，两个单摆A和B的摆长LA＞LB，将它们都拉离竖直方向一个很小的角度θ然后释放，那么这两个摆球到达最低点时的速度υ的大小和经历时间t应满足（ ）
如图所示，两个单摆A和B的摆长LA＞LB，将它们都拉离竖直方向一个很小的角度θ然后释放，那么这两个摆球到达最低点时的速度υ的大小和经历时间应满足（ ）| A、υA＜υB，tA＜tB | B、υA＜υB，tA＞tB | C、υA＞υB，tA＞tB | D、υA＞υB，tA＜tB |
如图所示，两个单摆A和B，其摆长LA＞LB，将它们都拉离竖直方向一个很小的角度
，然后由静止释放，那么两个球到达最低点时的速度大小与经历时间关系的多少为() 
| A．vA＞vB，tA＞tB | B．vA＜vB，tA＜tB |
| C．vA＞vB，tA＜tB | D．vA＜vB，tA＞tB |
，然后由静止释放，那么两个球到达最低点时的速度大小与经历时间关系的多少为() 
