题目内容
如图所示，长度为L的无动力翻滚过山车以某一初速度沿水平轨道运动，然后进入竖直平面内半径为R的圆轨道，如不计轨道间的摩擦，且L＞2πR，为使过山车能顺利通过圆形轨道，则过山车的初速度至少应为多大？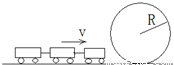
【答案】分析：过山车能顺利通过最高点，则在最高点重力提供向心力，求出最小速度，过山车全部通过最高点，在圆行轨道上的长度为2πR，此部分的重心离水平轨道高为R，过山车运动过程中机械能守恒，根据机械能守恒定律即可求解．
解答：解：设过山车能顺利通过最高点，至最高点的最小速度为v
则mg=m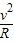
过山车全部通过最高点，在圆行轨道上的长度为2πR，
此部分的重心离水平轨道高为R，过山车运动过程中机械能守恒，
则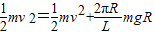
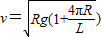
答：过山车的初速度至少应为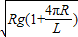
．
点评：本题主要考查了机械能守恒定律及圆周运动向心力公式的直接应用，注意重心位置的确定，难度适中．
解答：解：设过山车能顺利通过最高点，至最高点的最小速度为v
则mg=m
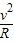
过山车全部通过最高点，在圆行轨道上的长度为2πR，
此部分的重心离水平轨道高为R，过山车运动过程中机械能守恒，
则
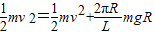
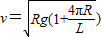
答：过山车的初速度至少应为
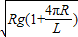．点评：本题主要考查了机械能守恒定律及圆周运动向心力公式的直接应用，注意重心位置的确定，难度适中．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
如图所示，长度为L的轻绳上端固定在O点，下端系一质量为m的小球（小球的大小可以忽略）． 由图示位置无初速度释放小球，求当小球通过最低点时的速度大小及轻绳对小球的拉力．（不计空气阻力）
（2008?韶关一模）如图所示，长度为L的轻杆上端连着一质量为m的体积可忽略的小重物B．杆的下端用铰链固接于水平面上的A点．同时，置于同一水平面上的立方体C恰与B接触，立方体C的质量为M．今做微小的扰动，使杆向右倾倒，设B与C、C与水平面间均无摩擦，而B与C刚脱离接触的瞬间，杆与地面夹角恰好为
（2011?北京）如图所示，长度为l的轻绳上端固定在O点，下端系一质量为m的小球（小球的大小可以忽略）．
（2012?西城区二模）如图所示，长度为l的轻绳上端固定在O点，下端系一质量为m，电荷量为+q的小球．整个装置处于水平向右，场强大小为
（2012?虹口区二模）如图所示，长度为l的绝缘轻杆一端可绕O点在竖直平面内自由转动，另一端固定一个质量为m、带电量为+q的小球，整个装置处于水平向右的匀强电场中，电场强度E=