题目内容

在光滑的绝缘水平地面上，有直径相同的两个金属小球a、b，如图示，已知ma=2mb=2m．a不带电，b带正电2q，初始时，球b静止在磁感应强度为B的匀强磁场中，球a以初速度v0进入磁场中与b正碰，碰后b球对水平地面的压力恰好为零．求：碰后a对水平地面的压力多大？
分析：A和C碰撞前后动量守恒，且碰后两球均分电荷，都将受到洛伦兹力，由左手定则判断洛伦兹力的方向
解答：解：a球匀速进入磁场与b球相碰，满足动量守恒，且碰后a、b的带电量均为q，设碰后a、b的速度分别为va，vb，规定向右为正方向，依动量守恒定律有：
mav0=mava+mbvb
对b球：qBvb=mbg
ma=2mb=2m
解得：va=v0-
mg
2Bq

对球a：FN=mag-qBva=
5
2
mg-qv0B
由牛顿第三定律有：FN=-F′N
故a球对水平面的压力为
5
2
mg-qv0B
答：碰后a对水平地面的压力为
5
2
mg-qv0B．
点评：抓住碰撞前后动量守恒，且碰后两球均带点，都受洛伦兹力，同时注意挖掘隐含条件．
练习册系列答案
相关题目
如图所示，水平地面M点左侧粗糙，右侧光滑．整个空间有一场强大小E1=1×103N/C、方向竖直向下的匀强电场．质量mA=0.04kg的不带电小物块A用长为R=5m不可伸长的绝缘轻质细绳拴于O点，静止时与地面刚好接触．带正电的小物块B与左端固定在墙上的绝缘轻弹簧接触但不粘连，B的质量mB=0.02kg，带电量为q=+2×10-4 C，与M左侧地面间动摩擦因数μ=0.5．现用水平向左的推力将B由M点（弹簧原长处）缓慢推至P点（弹簧仍在弹性限度内），推力做功W=2.65J，MP之间的距离为L=50cm．撤去推力，B向右运动，随后与A发生正碰并瞬间成为一个整体C（A、B、C均可视为质点）．已知碰撞前后电荷量保持不变，碰后C的速度为碰前B速度的
13
．碰后立即把匀强电场方向变为竖直向上，场强大小变为E2=6×103N/C．（取g=10m/s2）求：
（1）B与A碰撞过程中损失的机械能．
（2）碰后C是否立即做圆周运动？如果是，求C运动到最高点时绳的拉力大小；如果不是，则C运动到什么位置时绳子再次绷紧？
如图（a）所示，有两级光滑的绝缘平台，高一级平台距离绝缘板的中心O的高度为h，低一级平台高度是高一级平台高度的一半．绝缘板放在水平地面上，板与地面间的动摩擦因数为μ，一轻质弹簧一端连接在绝缘板的中心，另一端固定在墙面上．边界GH左边存在着正交的匀强电场和变化的磁场，电场强度为E，磁感应强度变化情况如图（b）所示，磁感应强度大小均为B．有一质量为m、带负电的小球从高一级平台左边缘以一定初速滑过平台后在t=0时刻垂直于边界GH进入复合场中，设小球刚进入复合场时磁场方向向外且为正值．小球做圆周运动至O点处恰好与绝缘板发生弹性碰撞，碰撞后小球立即垂直于边界GH返回并滑上低一级平台，绝缘板从C开始向右压缩弹簧的最大距离为S到达D，求：
（1）磁场变化的周期T．
（2）小球从高一级平台左边缘滑出的初速度v．
（3）绝缘板的质量M．
（4）绝缘板压缩弹簧具有的弹性势能EP．
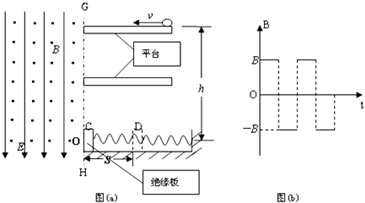
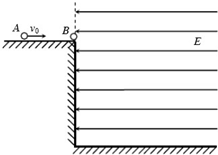精英家教网
如图（a）所示，有两级光滑的绝缘平台，高一级平台距离绝缘板的中心O的高度为h，低一级平台高度是高一级平台高度的一半．绝缘板放在水平地面上，板与地面间的动摩擦因数为μ，一轻质弹簧一端连接在绝缘板的中心，另一端固定在墙面上．边界GH左边存在着正交的匀强电场和交变磁场，电场强度为E，磁感应强度变化情况如图（b）所示，磁感强度大小均为B．有一质量为m、带负电的小球从高一级平台左边缘以一定初速滑过平台后垂直于边界GH进入复合场中，设小球刚进入复合场时磁场方向向外且为正值．小球运动至O点处恰好与绝缘板发生弹性正碰，碰撞后小球恰能垂直于边界GH返回低一级平台上，而绝缘板向右从C点运动到D点，C、D间的距离为S，求：
（1）交变磁场变化的周期T；
（2）小球从高一级平台左边缘滑上的初速度v；
（3）绝缘板的质量M；
（4）绝缘板从C点运动至D点时，弹簧具有的弹性势能EP．
精英家教网
如图（a）所示，有两级光滑的绝缘平台，高一级平台距离绝缘物块的中心O的高度为h，低一级平台高度是高一级平台高度的一半．绝缘物块放在水平地面上，物块与地面间的动摩擦力为f，一轻质弹簧一端连接在绝缘物块的中心，另一端固定在墙面上．边界GH左边存在着正交的匀强电场和交变磁场，电场强度为E，磁感应强度变化情况如图（b）所示，磁感强度大小均为B0．有一质量为m、带负电的小球从高一级平台左边缘以一定初速度滑过平台后，垂直于边界GH在t=T/4时刻进入复合场，刚进入复合场时磁场方向向外且为正值．小球以不变的速率运动至O点处恰好与绝缘物块发生正碰，碰撞过程没有能量损失（碰撞时间不计）．碰撞后小球恰能垂直于边界GH返回低一级平台上，而绝缘物块从C点向右运动到最远点D，C、D间的距离为S，（重力加速度为g）
求：
精英家教网
（1）交变磁场变化的周期T；
（2）小球从高一级平台左边缘滑出的初速度v；
（3）绝缘物块从C点运动至D点时，弹簧具有的弹性势能Ep．
精英家教网如图所示，一个光滑、绝缘水平高台的右面空间中存在范围足够大且水平向左的匀强电场，高台边缘静置一个带电量为+q、质量为m的小球B，另有一个绝缘不带电的小球A（大小与小球B相同，质量大于m）以初速度v0向B运动，A与B发生弹性碰撞后水平进入电场，发生再次碰撞后落到水平地面．已知匀强电场的电场场强为E=
2mgq
，重力加速度为g．（小球A、B碰撞过程中电荷不发生转移）
（1）如果小球A的质量为3m，求：
①小球A、B发生弹性碰撞（首次碰撞）后各自的速度；
②小球A、B再次碰撞前运动过程中相距的最大距离；
③B小球在电场中与A小球再次碰撞前具有的动能；
（2）如果保持B的质量不变，改变A的质量，其它条件不变，A、B小球再次碰撞前运动过程中相距的最大距离及再次碰撞发生的高度是否发生变化？试证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网