题目内容
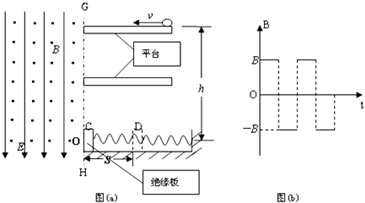
如图(a)所示,有两级光滑的绝缘平台,高一级平台距离绝缘物块的中心O的高度为h,低一级平台高度是高一级平台高度的一半.绝缘物块放在水平地面上,物块与地面间的动摩擦力为f,一轻质弹簧一端连接在绝缘物块的中心,另一端固定在墙面上.边界GH左边存在着正交的匀强电场和交变磁场,电场强度为E,磁感应强度变化情况如图(b)所示,磁感强度大小均为B0.有一质量为m、带负电的小球从高一级平台左边缘以一定初速度滑过平台后,垂直于边界GH在t=T/4时刻进入复合场,刚进入复合场时磁场方向向外且为正值.小球以不变的速率运动至O点处恰好与绝缘物块发生正碰,碰撞过程没有能量损失(碰撞时间不计).碰撞后小球恰能垂直于边界GH返回低一级平台上,而绝缘物块从C点向右运动到最远点D,C、D间的距离为S,(重力加速度为g)
求:

(1)交变磁场变化的周期T;
(2)小球从高一级平台左边缘滑出的初速度v;
(3)绝缘物块从C点运动至D点时,弹簧具有的弹性势能Ep.
求:

(1)交变磁场变化的周期T;
(2)小球从高一级平台左边缘滑出的初速度v;
(3)绝缘物块从C点运动至D点时,弹簧具有的弹性势能Ep.
分析:(1)带电小球进入复合场做匀速圆周运动,重力与电场力平衡,可得到场强.小球在t=
T时刻进入复合场,与物块碰后做匀速圆周运动,恰能垂直于边界GH返回低一级平台上,返回低一级台阶的过程,磁场方向与小球进入复合场时磁场方向相反,说明小球从高一级平台进入复合场到与物块碰撞经过的时间等于
,由小球做匀速圆周运动的周期公式T′=
即可求出交变磁场变化的周期T;
(2)小球在复合场中由洛伦兹力提供向心力,根据牛顿第二定律求解小球从高一级平台左边缘滑出的初速度v;
(3)根据牛顿第二定律求出小球与物块碰后的速率,根据能量守恒求出物块获得的动能,并由能量守恒求解绝缘物块从C点运动至D点时,弹簧具有的弹性势能Ep.
| 1 |
| 4 |
| T |
| 4 |
| 2πm |
| qB |
(2)小球在复合场中由洛伦兹力提供向心力,根据牛顿第二定律求解小球从高一级平台左边缘滑出的初速度v;
(3)根据牛顿第二定律求出小球与物块碰后的速率,根据能量守恒求出物块获得的动能,并由能量守恒求解绝缘物块从C点运动至D点时,弹簧具有的弹性势能Ep.
解答:解:(1)带电小球垂直于边界GH进入复合场,做匀速圆周运动,则有:
qE=mg…①
带电小球做匀速圆周运动由洛伦兹力提供向心力,且经过半个圆周运动到达O点,碰后再经过半个圆周回到二级平台.设小球做匀速圆周运动的周期为T′,则:
T′=
…②
因为
=
,得T=2T′,则由①②,得交变磁场变化的周期:T=
(2)由牛顿第二定律得:qvB0=m
…③
由几何关系得:r=
…④
由①③④,解得:v=
…⑤
(3)设小球碰后的速度大小为v′,碰后做匀速圆周运动的半径为r′,由牛顿第二定律得:
qv′B0=m
…⑥
由几何关系有:r′=
…⑦
联立解得:v′=
…⑧
设碰后物块获得的动能为Ek,因碰撞过程没有能量损失,则有:
mv2=
mv′2+Ek…⑨
物块从C到D过程,由能量守恒定律得:
Ek=fs+Ep…⑩
由⑤⑧⑨⑩解得:Ep=
-fs.
答:
(1)交变磁场变化的周期T为
;
(2)小球从高一级平台左边缘滑出的初速度v是
;
(3)绝缘物块从C点运动至D点时,弹簧具有的弹性势能Ep是
-fs.
qE=mg…①
带电小球做匀速圆周运动由洛伦兹力提供向心力,且经过半个圆周运动到达O点,碰后再经过半个圆周回到二级平台.设小球做匀速圆周运动的周期为T′,则:
T′=
| 2πm |
| qB |
因为
| T |
| 4 |
| T′ |
| 2 |
| 4πE |
| gB0 |
(2)由牛顿第二定律得:qvB0=m
| v2 |
| r |
由几何关系得:r=
| h |
| 2 |
由①③④,解得:v=
| gB0h |
| 2E |
(3)设小球碰后的速度大小为v′,碰后做匀速圆周运动的半径为r′,由牛顿第二定律得:
qv′B0=m
| v′2 |
| r′ |
由几何关系有:r′=
| h |
| 4 |
联立解得:v′=
| gB0h |
| 4E |
设碰后物块获得的动能为Ek,因碰撞过程没有能量损失,则有:
| 1 |
| 2 |
| 1 |
| 2 |
物块从C到D过程,由能量守恒定律得:
Ek=fs+Ep…⑩
由⑤⑧⑨⑩解得:Ep=
3mq2
| ||
| 32E2 |
答:
(1)交变磁场变化的周期T为
| 4πE |
| gB0 |
(2)小球从高一级平台左边缘滑出的初速度v是
| gB0h |
| 2E |
(3)绝缘物块从C点运动至D点时,弹簧具有的弹性势能Ep是
3mq2
| ||
| 32E2 |
点评:本题要通过分析,得到小球圆周运动的周期与交变磁场变化的周期T的关系,根据牛顿第二定律求出小球与物块碰撞前后的速率是常规方法.此题综合性较强.

练习册系列答案
相关题目