题目内容
如图所示,以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑水平地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C,一物块被轻放在水平匀速运动的传送带上E点,运动到A时刚好与传送带速度相同,然后经A沿半圆轨道滑下,再经B滑上滑板,滑板运动到C时被牢固粘连,物块可视为质点,质量为m,滑板质量M=2m,两半圆半径均为R,板长l=6.5R,板右端到C的距离L在R<L<5R范围内取值,E距A为S=5R,物块与传送带、物块与滑板间的动摩擦因数均μ=0.5,重力加速度取g.
(1)求物块滑到B点的速度大小;
(2)试讨论物块从滑上滑板到离开滑板右端的过程中,克服摩擦力做的功Wf与L的关系,并判断物块能否滑到CD轨道的中点.
(1)求物块滑到B点的速度大小;
(2)试讨论物块从滑上滑板到离开滑板右端的过程中,克服摩擦力做的功Wf与L的关系,并判断物块能否滑到CD轨道的中点.

(1)设物块运动到A和B点的速度分别为v1、v2,
由动能定理得μmgS=
m
…①
由机械能守恒定律
m
=2mgR+
m
…②
联立①②,得v2=3
…③
(2)设滑板与物块达到共同速度v3时,位移分别为l1、l2,
由动量守恒定律mv2=(m+M)v3…④
由动能定理 μmgl1=
M
…⑤
-μmgl2=
m
-
m
…⑥
联立③④⑤⑥,得 l1=2R l2=8R…⑦
物块相对滑板的位移△l=l2-l1 △l<l
即物块与滑板在达到相同共同速度时,物块未离开滑板…⑧
物块滑到滑板右端时
若R<L<2R,Wf=μmg(l+L)…⑨
Wf=
mg(13R+2L)…⑩
若2R≤L<5R,Wf=μmg(l+l1)…(11)
Wf=
mgR…(12)
设物块滑到C点的动能为Ek,
由动能定理 -Wf=Ek-
m
…(13)
L最小时,克服摩擦力做功最小,因为L>R,
由③⑩(13)确定Ek小于mgR,则物块不能滑到CD轨道中点.
答:(1)物块滑到B点的速度v2=3
(2)物块不能滑到CD轨道中点.
由动能定理得μmgS=
| 1 |
| 2 |
| v | 21 |
由机械能守恒定律
| 1 |
| 2 |
| v | 22 |
| 1 |
| 2 |
| v | 21 |
联立①②,得v2=3
| gR |
(2)设滑板与物块达到共同速度v3时,位移分别为l1、l2,
由动量守恒定律mv2=(m+M)v3…④
由动能定理 μmgl1=
| 1 |
| 2 |
| v | 23 |
-μmgl2=
| 1 |
| 2 |
| v | 23 |
| 1 |
| 2 |
| v | 22 |
联立③④⑤⑥,得 l1=2R l2=8R…⑦
物块相对滑板的位移△l=l2-l1 △l<l
即物块与滑板在达到相同共同速度时,物块未离开滑板…⑧
物块滑到滑板右端时
若R<L<2R,Wf=μmg(l+L)…⑨
Wf=
| 1 |
| 4 |
若2R≤L<5R,Wf=μmg(l+l1)…(11)
Wf=
| 17 |
| 4 |
设物块滑到C点的动能为Ek,
由动能定理 -Wf=Ek-
| 1 |
| 2 |
| v | 22 |
L最小时,克服摩擦力做功最小,因为L>R,
由③⑩(13)确定Ek小于mgR,则物块不能滑到CD轨道中点.
答:(1)物块滑到B点的速度v2=3
| gR |
(2)物块不能滑到CD轨道中点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,以A、B和C、D为端点的半径为R=0.6m的两半圆形光滑绝缘轨道固定于竖直平面内,B端、C端与光滑绝缘水平面平滑连接.A端、D端之间放一绝缘水平传送带,传送带下方B、C之间的区域存在水平向右的匀强电场,场强E=5×105V/m.当传送带以v0=6m/s 的速度沿图示方向匀速运动时,将质量为m=4×10-3kg,带电量q=+1×10-8C的小物块由静止放上传送带的最右端,小物块第一次运动到传送带最左端时恰好能从A点沿半圆轨道滑下,不计小物块大小及传送带与半圆轨道间的距离,g取10m/s2,已知A、D端之间的距离为1.2m 等于水平传送带的长.
如图所示,以A、B和C、D为端点的半径为R=0.6m的两半圆形光滑绝缘轨道固定于竖直平面内,B端、C端与光滑绝缘水平面平滑连接.A端、D端之间放一绝缘水平传送带,传送带下方B、C之间的区域存在水平向右的匀强电场,场强E=5×105V/m.当传送带以v0=6m/s 的速度沿图示方向匀速运动时,将质量为m=4×10-3kg,带电量q=+1×10-8C的小物块由静止放上传送带的最右端,小物块第一次运动到传送带最左端时恰好能从A点沿半圆轨道滑下,不计小物块大小及传送带与半圆轨道间的距离,g取10m/s2,已知A、D端之间的距离为1.2m 等于水平传送带的长. (2011?广东)如图所示,以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑水平地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C,一物块被轻放在水平匀速运动的传送带上E点,运动到A时刚好与传送带速度相同,然后经A沿半圆轨道滑下,再经B滑上滑板,滑板运动到C时被牢固粘连,物块可视为质点,质量为m,滑板质量M=2m,两半圆半径均为R,板长l=6.5R,板右端到C的距离L在R<L<5R范围内取值,E距A为S=5R,物块与传送带、物块与滑板间的动摩擦因数均μ=0.5,重力加速度取g.
(2011?广东)如图所示,以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑水平地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C,一物块被轻放在水平匀速运动的传送带上E点,运动到A时刚好与传送带速度相同,然后经A沿半圆轨道滑下,再经B滑上滑板,滑板运动到C时被牢固粘连,物块可视为质点,质量为m,滑板质量M=2m,两半圆半径均为R,板长l=6.5R,板右端到C的距离L在R<L<5R范围内取值,E距A为S=5R,物块与传送带、物块与滑板间的动摩擦因数均μ=0.5,重力加速度取g.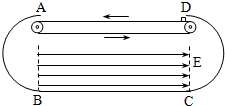 如图所示,以A、B和C、D为端点的半径为R=0.6m的两半圆形光滑绝缘轨道固定于竖直平面内,B端、C端与光滑绝缘水平地面平滑连接.A端、D端之间放一绝缘水平传送带.传送带下方B、C之间的区域存在水平向右的匀强电场,场强E=5×105V/m.当传送带以6m/s的速度沿图示方向匀速运动时,现将质量为m=4×10-3kg,带电量q=+1×10-8C的物块从传送带的右端由静止放上传送带.小物块运动第一次到A时刚好能沿半圆轨道滑下.不计小物块大小及传送带与半圆轨道间的距离,g取10m/s2,已知A、D端之间的距离为1.2m.求:
如图所示,以A、B和C、D为端点的半径为R=0.6m的两半圆形光滑绝缘轨道固定于竖直平面内,B端、C端与光滑绝缘水平地面平滑连接.A端、D端之间放一绝缘水平传送带.传送带下方B、C之间的区域存在水平向右的匀强电场,场强E=5×105V/m.当传送带以6m/s的速度沿图示方向匀速运动时,现将质量为m=4×10-3kg,带电量q=+1×10-8C的物块从传送带的右端由静止放上传送带.小物块运动第一次到A时刚好能沿半圆轨道滑下.不计小物块大小及传送带与半圆轨道间的距离,g取10m/s2,已知A、D端之间的距离为1.2m.求: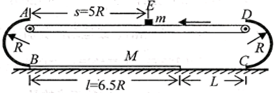 如图所示,以A、B和C、D为断点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑的地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C两点,一物块(视为质点)被轻放在水平匀速运动的传送带上E点,运动到A点时刚好与传送带速度相同,然后经A点沿半圆轨道滑下,再经B点滑上滑板,滑板运动到C点时被牢固粘连.物块可视为质点,质量为m,滑板质量为M=2m,两半圆半径均为R,板长l=6.5R,板右端到C点的距离L在R<L<5R范围内取值,E点距A点的距离s=5R,物块与传送带、物块与滑板间的动摩擦因数均为μ=0.5,重力加速度g已知.
如图所示,以A、B和C、D为断点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑的地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C两点,一物块(视为质点)被轻放在水平匀速运动的传送带上E点,运动到A点时刚好与传送带速度相同,然后经A点沿半圆轨道滑下,再经B点滑上滑板,滑板运动到C点时被牢固粘连.物块可视为质点,质量为m,滑板质量为M=2m,两半圆半径均为R,板长l=6.5R,板右端到C点的距离L在R<L<5R范围内取值,E点距A点的距离s=5R,物块与传送带、物块与滑板间的动摩擦因数均为μ=0.5,重力加速度g已知.