题目内容
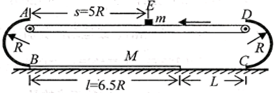 如图所示,以A、B和C、D为断点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑的地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C两点,一物块(视为质点)被轻放在水平匀速运动的传送带上E点,运动到A点时刚好与传送带速度相同,然后经A点沿半圆轨道滑下,再经B点滑上滑板,滑板运动到C点时被牢固粘连.物块可视为质点,质量为m,滑板质量为M=2m,两半圆半径均为R,板长l=6.5R,板右端到C点的距离L在R<L<5R范围内取值,E点距A点的距离s=5R,物块与传送带、物块与滑板间的动摩擦因数均为μ=0.5,重力加速度g已知.
如图所示,以A、B和C、D为断点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑的地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C两点,一物块(视为质点)被轻放在水平匀速运动的传送带上E点,运动到A点时刚好与传送带速度相同,然后经A点沿半圆轨道滑下,再经B点滑上滑板,滑板运动到C点时被牢固粘连.物块可视为质点,质量为m,滑板质量为M=2m,两半圆半径均为R,板长l=6.5R,板右端到C点的距离L在R<L<5R范围内取值,E点距A点的距离s=5R,物块与传送带、物块与滑板间的动摩擦因数均为μ=0.5,重力加速度g已知.(1)求物块滑到B点的速度大小;
(2)求物块滑到B点时对半圆轨道的压力;
(3)物块在滑板上滑动过程中,当物块与滑板达到共同速度时,测得它们的共同速度为u=
| uB | 3 |
分析:(1)物块从E到B点由动能定理可求得到达B点的速度;
(2)在B点由牛顿第二定律求的对半圆轨道的压力;
(3)当达到共同速度时通过动能定理判断出滑块和木板前进的位移,然后通过讨论L的大小判断出摩擦力做的功Wf与L的关系.并判断物块能否滑到CD轨道的中点.
(2)在B点由牛顿第二定律求的对半圆轨道的压力;
(3)当达到共同速度时通过动能定理判断出滑块和木板前进的位移,然后通过讨论L的大小判断出摩擦力做的功Wf与L的关系.并判断物块能否滑到CD轨道的中点.
解答:解(1)设物块滑到B点的速度大小为vB,对物体从E到B过程,根据动能定理得:
μmgs+2mgR =
.
解得:vB =3
.
(2)物块在B点时,根据牛顿第二定律得:FN -mg=m
.
解得:FN=m
+mg=10mg.
(3)物块从B滑上滑板后开始作匀减速运动,此时滑板开始作匀加速直线运动,当物块与滑板达共同速度时,二者开始作匀速运动.由题意知它们的共同速度为:v=
.
此过程,对物块据动能定理得:-μmgs1=
-
.
解得:s1=8R.
此过程,对滑板据动能定理得:μmgs2=
mv2-0.
解得:s2=2R.
由此可知物块在滑板上滑过s1-s2=6R时,二者就具有共同速度了.因为6R<6.5R,所以物块并没有从滑板上滑下去.
讨论:
当R<L<2R时,物块在滑板上一直匀减速运动至右端,运动的位移为6.5R+L,克服摩擦力做的功为:Wf=μmg(6.5R+L)=
mg(13R+2L).
设滑上C点的速度为vc,对物块根据动能定理得:
-μmg(6.5R+L)=
-
解得:
=
mg(2.5R-L)<mgR,所以物块不可能滑到CD轨道的中点.
当2R≤L<5R时,物块的运动的匀减速运动8R,匀速运动L-2R,再匀减速运动0.5R,克服摩擦力做的功为:Wf=μmg(8R+0.5R)=
mgR.
-Wf=
-
解得:
=
mgR<mgR,所以物块不能滑到CD轨道的中点.
答:(1)求物块滑到B点的速度大小为3
;
(2)求物块滑到B点时对半圆轨道的压力10mg;
(3)当R<L<2R时,克服摩擦力做功为
mg(13R+2L),不能滑到CD的中点;
当2R≤L<5R时,克服摩擦力做功为
mgR,不能滑到CD的中点;
μmgs+2mgR =
| 1 |
| 2 |
| mv | 2 B |
解得:vB =3
| gR |
(2)物块在B点时,根据牛顿第二定律得:FN -mg=m
| ||
| R |
解得:FN=m
| ||
| R |
(3)物块从B滑上滑板后开始作匀减速运动,此时滑板开始作匀加速直线运动,当物块与滑板达共同速度时,二者开始作匀速运动.由题意知它们的共同速度为:v=
| vB |
| 3 |
此过程,对物块据动能定理得:-μmgs1=
| 1 |
| 2 |
| mv | 2 |
| 1 |
| 2 |
| mv | 2 B |
解得:s1=8R.
此过程,对滑板据动能定理得:μmgs2=
| 1 |
| 2 |
解得:s2=2R.
由此可知物块在滑板上滑过s1-s2=6R时,二者就具有共同速度了.因为6R<6.5R,所以物块并没有从滑板上滑下去.
讨论:
当R<L<2R时,物块在滑板上一直匀减速运动至右端,运动的位移为6.5R+L,克服摩擦力做的功为:Wf=μmg(6.5R+L)=
| 1 |
| 4 |
设滑上C点的速度为vc,对物块根据动能定理得:
-μmg(6.5R+L)=
| 1 |
| 2 |
| mv | 2 c |
| 1 |
| 2 |
| mv | 2 B |
解得:
| 1 |
| 2 |
| mv | 2 c |
| 1 |
| 2 |
当2R≤L<5R时,物块的运动的匀减速运动8R,匀速运动L-2R,再匀减速运动0.5R,克服摩擦力做的功为:Wf=μmg(8R+0.5R)=
| 17 |
| 4 |
-Wf=
| 1 |
| 2 |
| mv | ′2 c |
| 1 |
| 2 |
| mv | 2 B |
解得:
| 1 |
| 2 |
| mv | ′2 c |
| 1 |
| 4 |
答:(1)求物块滑到B点的速度大小为3
| gR |
(2)求物块滑到B点时对半圆轨道的压力10mg;
(3)当R<L<2R时,克服摩擦力做功为
| 1 |
| 4 |
当2R≤L<5R时,克服摩擦力做功为
| 17 |
| 4 |
点评:本题考查机械能守恒以及有摩擦的板块模型中克服摩擦力做的功.判断物块与滑板在达到相同共同速度时,物块未离开滑板是关键,是一道比较困难的好题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 如图所示,以A、B和C、D为端点的半径为R=0.6m的两半圆形光滑绝缘轨道固定于竖直平面内,B端、C端与光滑绝缘水平面平滑连接.A端、D端之间放一绝缘水平传送带,传送带下方B、C之间的区域存在水平向右的匀强电场,场强E=5×105V/m.当传送带以v0=6m/s 的速度沿图示方向匀速运动时,将质量为m=4×10-3kg,带电量q=+1×10-8C的小物块由静止放上传送带的最右端,小物块第一次运动到传送带最左端时恰好能从A点沿半圆轨道滑下,不计小物块大小及传送带与半圆轨道间的距离,g取10m/s2,已知A、D端之间的距离为1.2m 等于水平传送带的长.
如图所示,以A、B和C、D为端点的半径为R=0.6m的两半圆形光滑绝缘轨道固定于竖直平面内,B端、C端与光滑绝缘水平面平滑连接.A端、D端之间放一绝缘水平传送带,传送带下方B、C之间的区域存在水平向右的匀强电场,场强E=5×105V/m.当传送带以v0=6m/s 的速度沿图示方向匀速运动时,将质量为m=4×10-3kg,带电量q=+1×10-8C的小物块由静止放上传送带的最右端,小物块第一次运动到传送带最左端时恰好能从A点沿半圆轨道滑下,不计小物块大小及传送带与半圆轨道间的距离,g取10m/s2,已知A、D端之间的距离为1.2m 等于水平传送带的长. (2011?广东)如图所示,以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑水平地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C,一物块被轻放在水平匀速运动的传送带上E点,运动到A时刚好与传送带速度相同,然后经A沿半圆轨道滑下,再经B滑上滑板,滑板运动到C时被牢固粘连,物块可视为质点,质量为m,滑板质量M=2m,两半圆半径均为R,板长l=6.5R,板右端到C的距离L在R<L<5R范围内取值,E距A为S=5R,物块与传送带、物块与滑板间的动摩擦因数均μ=0.5,重力加速度取g.
(2011?广东)如图所示,以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑水平地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C,一物块被轻放在水平匀速运动的传送带上E点,运动到A时刚好与传送带速度相同,然后经A沿半圆轨道滑下,再经B滑上滑板,滑板运动到C时被牢固粘连,物块可视为质点,质量为m,滑板质量M=2m,两半圆半径均为R,板长l=6.5R,板右端到C的距离L在R<L<5R范围内取值,E距A为S=5R,物块与传送带、物块与滑板间的动摩擦因数均μ=0.5,重力加速度取g.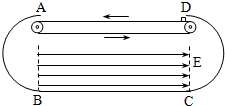 如图所示,以A、B和C、D为端点的半径为R=0.6m的两半圆形光滑绝缘轨道固定于竖直平面内,B端、C端与光滑绝缘水平地面平滑连接.A端、D端之间放一绝缘水平传送带.传送带下方B、C之间的区域存在水平向右的匀强电场,场强E=5×105V/m.当传送带以6m/s的速度沿图示方向匀速运动时,现将质量为m=4×10-3kg,带电量q=+1×10-8C的物块从传送带的右端由静止放上传送带.小物块运动第一次到A时刚好能沿半圆轨道滑下.不计小物块大小及传送带与半圆轨道间的距离,g取10m/s2,已知A、D端之间的距离为1.2m.求:
如图所示,以A、B和C、D为端点的半径为R=0.6m的两半圆形光滑绝缘轨道固定于竖直平面内,B端、C端与光滑绝缘水平地面平滑连接.A端、D端之间放一绝缘水平传送带.传送带下方B、C之间的区域存在水平向右的匀强电场,场强E=5×105V/m.当传送带以6m/s的速度沿图示方向匀速运动时,现将质量为m=4×10-3kg,带电量q=+1×10-8C的物块从传送带的右端由静止放上传送带.小物块运动第一次到A时刚好能沿半圆轨道滑下.不计小物块大小及传送带与半圆轨道间的距离,g取10m/s2,已知A、D端之间的距离为1.2m.求: