题目内容
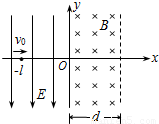 如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区的右边界.现有一质量为m.电量为-q的带电粒子,从电场中的P点以初速度V沿x轴正方向开始运动,已知P点的坐标为(-L,0)且
如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区的右边界.现有一质量为m.电量为-q的带电粒子,从电场中的P点以初速度V沿x轴正方向开始运动,已知P点的坐标为(-L,0)且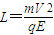 ,(不计带电粒子的重力)试求:
,(不计带电粒子的重力)试求:(1)带电粒子运动到Y轴上时的速度;
(2)要使带电粒子能穿越磁场区域而不再返回到电场中,磁场的宽度最大为多少.
【答案】分析:(1)粒子在电场中受到的电场力的方向向上,粒子做的事类平抛运动,水平方向做的是匀速运动,竖直方向做的是匀加速直线运动,从而可以求得带电粒子运动到Y轴上时的速度;
(2)当磁场的运动的轨迹恰好与磁场的有边沿相切时,此时的磁场的宽度最大,根据粒子的运动的轨迹可以求得磁场的宽度最大值.
解答:解:(1)粒子在电场中做类平抛运动,
竖直速度Vy=at,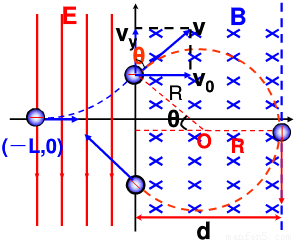
加速度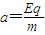
水平位移L=Vt,
由以上各式得进入电场时的合速度为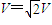 ,
,
方向与y轴成45,
(2)带电粒子在磁场中做匀速圆周运动
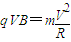
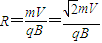 ,与右边界相切时,
,与右边界相切时,
由几何关系得Rsin45°+R=d,
解得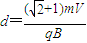 ,
,
故磁场的宽度最大为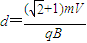 .
.
点评:本题考查带电粒子在匀强磁场中的运动,要掌握住半径公式、周期公式,画出粒子的运动轨迹后,几何关系就比较明显了.
(2)当磁场的运动的轨迹恰好与磁场的有边沿相切时,此时的磁场的宽度最大,根据粒子的运动的轨迹可以求得磁场的宽度最大值.
解答:解:(1)粒子在电场中做类平抛运动,
竖直速度Vy=at,

加速度
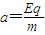
水平位移L=Vt,
由以上各式得进入电场时的合速度为
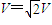 ,
,方向与y轴成45,
(2)带电粒子在磁场中做匀速圆周运动
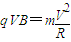
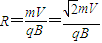 ,与右边界相切时,
,与右边界相切时,由几何关系得Rsin45°+R=d,
解得
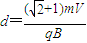 ,
,故磁场的宽度最大为
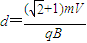 .
.点评:本题考查带电粒子在匀强磁场中的运动,要掌握住半径公式、周期公式,画出粒子的运动轨迹后,几何关系就比较明显了.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?青铜峡市一模)如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区的右边界.现有一质量为m.电量为-q的带电粒子,从电场中的P点以初速度V0沿x轴正方向开始运动,已知P点的坐标为(-L,0)且
(2011?青铜峡市一模)如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区的右边界.现有一质量为m.电量为-q的带电粒子,从电场中的P点以初速度V0沿x轴正方向开始运动,已知P点的坐标为(-L,0)且 (2007?河东区模拟)如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区域的右边界.现有一质量为m,电荷量为-q的带电粒子从电场中坐标位置(-L,0)处,以初速度v0沿x轴正方向开始运动,且已知
(2007?河东区模拟)如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区域的右边界.现有一质量为m,电荷量为-q的带电粒子从电场中坐标位置(-L,0)处,以初速度v0沿x轴正方向开始运动,且已知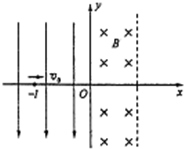 如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界线,图中虚线为磁场区域的右边界,现有一质量为m、电荷量为-q的带电粒子从电场中坐标位置(-l,0)处,以初速度v0沿x轴正方向开始运动,且已知
如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界线,图中虚线为磁场区域的右边界,现有一质量为m、电荷量为-q的带电粒子从电场中坐标位置(-l,0)处,以初速度v0沿x轴正方向开始运动,且已知