题目内容
宇航员站在一星球表面上的某高处，沿水平方向抛出一个小球，经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L.若抛出时的初速度增大为原来的2倍，则抛出点与落地点之间的距离为
L.已知两落地点在同一水平面上，该星球的半径为R，万有引力常量为G，求该星球的质量M.
【答案】
M=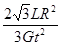
【解析】设抛出点的高度为H，第一次平抛的水平射程为x，则有
x2+H2=L2①
由平抛运动规律得知，当初速度增大为原来的2倍，其水平射程也增大到2x,可得
(2x)2+H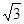2=(
L)2②
由方程①②解得H=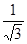
L
设该星球上的“重力加速度”为g，由平抛运动的规律得
H=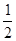
gt2③
由万有引力定律与牛顿第二定律得
mg=G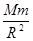
④
式中m为小球的质量，联立以上各式，得
M=.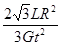
思路分析：抛出点的高度为H，第一次平抛的水平射程为x，则有x2+H2=L2初速度增大为原来的2倍，其水平射程也增大到2x,可得(2x)2+H2=(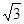L)2，再结合公式H=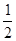gt2，mg=G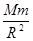，即可算出该星球的质量
试题点评：本题结合运动学规律考查了万有引力公式的应用，是一道小型的综合题，从运动学的角度打开一个突破口，进行解题
练习册系列答案
相关题目