题目内容
5.如图所示,在水平光滑轨道上停着甲、乙两辆实验小车,甲车系一穿过打点计时器的纸带,当甲车受到水平向右的瞬时作用力时,随即启动打点计时器,甲车运动一段距离后,与静止的乙车发生正碰并粘在一起运动,纸带记录下碰撞前甲车和碰撞后两车的运动情况,如图乙所示,电源频率为50Hz,甲车的质量m甲=2kg,求:
①乙车的质量m乙;
②两车碰撞时内能的增加量△E.
分析 根据纸带求出碰前甲车的速度和碰撞后一起运动的速度,结合动量守恒定律求出乙车的质量.根据能量守恒定律求出两车碰撞时内能的增加量.
解答 解:由题图可知,碰前甲车运动的速度大小为
v甲=$\frac{0.024}{0.04}m/s$=0.6 m/s
碰后甲、乙两车一起运动的速度大小为
v共=$\frac{0.016}{0.04}m/s$=0.4 m/s
由动量守恒定律可得:m甲v甲=(m甲+m乙)v共
代入数据得:m乙=1 kg
两车碰撞时内能的增加△E=△Ek=$\frac{1}{2}$m甲v甲2-$\frac{1}{2}$(m甲+m乙)v共2
代入数据可得:△E=0.12 J.
答:①乙车的质量为1kg;
②两车碰撞时内能的增加量△E为0.12J.
点评 本题考查了动量守恒定律和能量守恒定律的综合运用,知道甲乙两车碰撞的过程中动量守恒,结合碰撞前后速度求解质量,基础题.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
16.下列说法正确的是( )
| A. | 一个气体分子的体积等于气体的摩尔体积与阿伏加德罗常数之比 | |
| B. | 分子间相互作用的引力和斥力一定随分子间的距离增大而减小 | |
| C. | 气体分子热运动的平均动能减小,气体的压强一定减小 | |
| D. | 分子势能随分子间距离的增大可能增大、也可能减少 |
10.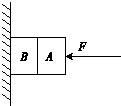 如图所示,初始时A、B两木块在水平方向的外力作用下挤压在竖直墙面上处于静止状态,A与B、B与墙面之间的动摩擦因数为μ=0.1,且最大静摩擦力等于滑动摩擦.两木块质量相等,都为1kg,当外力F变为下列不同值时,关于A、B之间的摩擦力f1,B与墙壁之间的摩擦力f2的大小,下列说法正确的是(g取10m/s2)( )
如图所示,初始时A、B两木块在水平方向的外力作用下挤压在竖直墙面上处于静止状态,A与B、B与墙面之间的动摩擦因数为μ=0.1,且最大静摩擦力等于滑动摩擦.两木块质量相等,都为1kg,当外力F变为下列不同值时,关于A、B之间的摩擦力f1,B与墙壁之间的摩擦力f2的大小,下列说法正确的是(g取10m/s2)( )
 如图所示,初始时A、B两木块在水平方向的外力作用下挤压在竖直墙面上处于静止状态,A与B、B与墙面之间的动摩擦因数为μ=0.1,且最大静摩擦力等于滑动摩擦.两木块质量相等,都为1kg,当外力F变为下列不同值时,关于A、B之间的摩擦力f1,B与墙壁之间的摩擦力f2的大小,下列说法正确的是(g取10m/s2)( )
如图所示,初始时A、B两木块在水平方向的外力作用下挤压在竖直墙面上处于静止状态,A与B、B与墙面之间的动摩擦因数为μ=0.1,且最大静摩擦力等于滑动摩擦.两木块质量相等,都为1kg,当外力F变为下列不同值时,关于A、B之间的摩擦力f1,B与墙壁之间的摩擦力f2的大小,下列说法正确的是(g取10m/s2)( )| A. | 当F=0时,f1=f2=10N | B. | 当F=50N时,f1=0,f2=5N | ||
| C. | 当F=100N时,f1=5N,f2=10N | D. | 当F=300N时,f1=10N,f2=20N |
12.关于平抛运动,下列说法错误的是( )
| A. | 平抛物体在运动过程中,其加速度和水平速度保持不变 | |
| B. | 平抛物体可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动 | |
| C. | 平抛物体是做曲线运动的,因此它不可能是匀变速运动 | |
| D. | 平抛物体水平飞行的距离与初速度和高度有关有关 |

 在光滑的水平地面上静止着一质量M=0.4kg的薄木板,一个质量m=0.2kg的木块(可视为质点)以v0=4m/s的速度,从木板左端滑上,一段时间后,又从木板上滑下(不计木块滑下时的机械能损失),两物体仍沿直线继续向前运动,从木块与木板刚刚分离开始计时,经时间t=3.0s,两物体之间的距离增加了s=3m,已知木块与木板的动摩擦因数μ=0.4,求薄木板的长度.
在光滑的水平地面上静止着一质量M=0.4kg的薄木板,一个质量m=0.2kg的木块(可视为质点)以v0=4m/s的速度,从木板左端滑上,一段时间后,又从木板上滑下(不计木块滑下时的机械能损失),两物体仍沿直线继续向前运动,从木块与木板刚刚分离开始计时,经时间t=3.0s,两物体之间的距离增加了s=3m,已知木块与木板的动摩擦因数μ=0.4,求薄木板的长度.