题目内容
11．
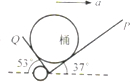送水员用双轮小车运送桶装水，以5m/s2的加速度水平向右匀加速直线运动，小车拉杆与水平面成37°角，如图所示．已知桶装水的总质量为20kg，不计桶与小车之间的摩擦，重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8，下列说法正确的是（ ）| A． | 小车P侧轨道对桶的支持力大小为160N | |
| B． | 小车Q侧轨道对桶的支持力大小为120N | |
| C． | 桶对小车辆侧轨道的压力大小之比为Fp：Fq=1：2 | |
| D． | 桶对小车辆侧轨道的压力大小之比为Fp：Fq=4：3 |
分析 对桶进行受力分析，受到重力、P、Q对桶的支持力作用，根据正交分解法结合牛顿第二定律列式即可求解．
解答 
解：对桶进行受力分析，如图所示：
竖直方向受力平衡，则有：mg=FQsin37°+FPsin53°
水平方向，根据牛顿第二定律得：
FQcos37°-FPcos53°=ma
带入数据得：
0.6FQ+0.8FP=10m…①，
0.8FQ-0.6FP=5m…②
由①②解得：$\frac{{F}_{P}}{{F}_{Q}}$=$\frac{1}{2}$，由于不知道水桶和水的质量，所以无法求出两个侧面对桶的支持力大小，故C正确，ABD错误．
故选：C．
点评 本题的关键是正确对物体进行受力分析，注意题目中给出的质量是小车和桶装矿泉水的总质量，不是桶装矿泉水的质量，不能求出两个侧面对桶的支持力大小，难度适中．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．下列有关惯性的说法正确的是（ ）
| A． | 牛顿第一定律给出了惯性的概念 | |
| B． | 任何有质量的物体都一定有惯性 | |
| C． | 对同一个物体而言，施加的外力越大，该物体的状态改变的越快，说明惯性与物体的受力有关 | |
| D． | 物体运动的速度越大，速度变为零需要的时间越长，说明物体的惯性与速度有关 |
2．
如图所示，在粗糙水平地面上放着圆柱状钢管A，A与竖直墙之间放着圆柱状钢管B，两钢管都处于静止状态．已知竖直墙面光滑，A、B外径都是D，质量都是M，其中钢管A的轴线到墙的水平距离为D，则（ ）
如图所示，在粗糙水平地面上放着圆柱状钢管A，A与竖直墙之间放着圆柱状钢管B，两钢管都处于静止状态．已知竖直墙面光滑，A、B外径都是D，质量都是M，其中钢管A的轴线到墙的水平距离为D，则（ ）| A． | 钢管A对地面的压力大小为2Mg | |
| B． | 钢管B对墙的压力大小为$\sqrt{3}$Mg | |
| C． | 钢管A对地面的摩擦力大小为$\frac{\sqrt{3}}{3}$Mg | |
| D． | 钢管A与钢管B之间作用力大小为$\frac{\sqrt{3}}{3}$Mg |
19．某物体沿平直路面上运动的s-t图象如图所示，则该物体（ ）
| A． | 15s末的位移为300m | B． | 前10s内的速度为3m/s | ||
| C． | 前10s内的加速度为3m/s2 | D． | 前25s内做单方向直线运动 |
6．
如图所示，一倾斜的传送带沿顺时针方向匀速转动，将物体轻放在传送带的上端和下端，下列说法正确的是（ ）
如图所示，一倾斜的传送带沿顺时针方向匀速转动，将物体轻放在传送带的上端和下端，下列说法正确的是（ ）| A． | 物体受到的摩擦力的方向均向上 | |
| B． | 物体受到的摩擦力的方向均向下 | |
| C． | 放上端时，物体受到的摩擦力的方向向上；放下端时，物体受到的摩擦力的方向向下 | |
| D． | 放上端时，物体受到的摩擦力的方向向下；放下端时，物体受到的摩擦力的方向向上 |
如图所示，车载升降平台将货物竖直匀速举起，同时车向右匀加速直线运动，下列描绘货物相对于地面的运动轨迹，正确的是（ ）
