题目内容
18.如图所示,直线MN上方为磁感应强度为B的足够大的匀强磁场.一电子(质量为m、电荷量为e)以v的速度从点O与MN成30°角的方向射入磁场中,求:
(1)确定大致的圆心位置,并用圆规画出轨迹;
(2)电子从磁场中射出时距O点多远;
(3)电子在磁场中运动的时间为多少.
分析 (1)洛伦兹力提供向心力,故圆心在与速度垂直的方向上;
(2)根据粒子在磁场中运动的半径公式得出半径的大小,结合几何关系求出电子从磁场中射出时距O点的距离;
(3)根据粒子在磁场中运动的周期公式,结合圆心角的大小,根据t=$\frac{θ}{2π}$求出电子在磁场中运动的时间.
解答 解:(1)轨迹如图:
(2)对电子在做圆周运动的过程中,设半径为r,有:
qvB=m$\frac{{v}^{2}}{r}$
所以:
r=$\frac{mv}{qB}$
结合几何关系可解得圆心角为60°,则电子出射点距O点的距离等于电子的运动半径为$\frac{mv}{qB}$.
(3)电子在磁场中的运动周期T为:
T=$\frac{2πr}{v}$
运动的时间为:
t=$\frac{\frac{π}{3}}{2π}T$
所以:
t=$\frac{πm}{3qB}$
答:(1)轨迹如图所示;
(2)电子从磁场中射出时距O点$\frac{mv}{qB}$远;
(3)电子在磁场中运动的时间为$\frac{πm}{3qB}$.
点评 解决本题的关键掌握带电粒子在磁场中运动的半径公式和周期公式,结合几何关系进行求解,掌握圆心、半径的确定方法.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
8. 翼装飞行(WingsuitFlying)是指运动员穿戴着拥有双翼的飞行服装和降落伞设备,运动员从高处一跃而下,用身体进行无动力空中飞行的运动,当到达安全极限的高度,运动员将打开降落伞平稳着落.一质量为m的极限运动员下降到极限高度时打开降落伞,而后做减速运动,设空气对他的阻力大小恒为F,那么在他减速下降h的过程中(g为当地的重力加速度).下列说法正确的是( )
翼装飞行(WingsuitFlying)是指运动员穿戴着拥有双翼的飞行服装和降落伞设备,运动员从高处一跃而下,用身体进行无动力空中飞行的运动,当到达安全极限的高度,运动员将打开降落伞平稳着落.一质量为m的极限运动员下降到极限高度时打开降落伞,而后做减速运动,设空气对他的阻力大小恒为F,那么在他减速下降h的过程中(g为当地的重力加速度).下列说法正确的是( )
 翼装飞行(WingsuitFlying)是指运动员穿戴着拥有双翼的飞行服装和降落伞设备,运动员从高处一跃而下,用身体进行无动力空中飞行的运动,当到达安全极限的高度,运动员将打开降落伞平稳着落.一质量为m的极限运动员下降到极限高度时打开降落伞,而后做减速运动,设空气对他的阻力大小恒为F,那么在他减速下降h的过程中(g为当地的重力加速度).下列说法正确的是( )
翼装飞行(WingsuitFlying)是指运动员穿戴着拥有双翼的飞行服装和降落伞设备,运动员从高处一跃而下,用身体进行无动力空中飞行的运动,当到达安全极限的高度,运动员将打开降落伞平稳着落.一质量为m的极限运动员下降到极限高度时打开降落伞,而后做减速运动,设空气对他的阻力大小恒为F,那么在他减速下降h的过程中(g为当地的重力加速度).下列说法正确的是( )| A. | 他的动能减少了Fh | B. | 他的重力势能减少了(F-mg)h | ||
| C. | 他的机械能减少了Fh | D. | 他的机械能减少了(F-mg)h |
9.短跑运动员在100m 竞赛中,测得他5s末的速度为10.4m/s,10s末到达终点的速度是10.2m/s,则运动员在这100m中的平均速度为( )
| A. | 10.0m/s | B. | 10.2m/s | C. | 10.3m/s | D. | 10.4m/s |
6.关于物理学史,下列说法中,不正确的是( )
| A. | 电荷量e的数值最早是由美国物理学家密立根测得的 | |
| B. | 法拉第首先发现了“磁生电”现象 | |
| C. | 法拉第通过实验研究确认了真空中两点电荷之间相互作用力的规律 | |
| D. | 库仑在前人工作的基础上,通过实验确认了真空中两个静止点电荷之间的相互作用力的规律 |
13. 如图所示,一带电油滴Q悬浮在平行板电容器两极板A、B之间,处于静止状态.下列做法中,能使 Q仍保持静止的有( )
如图所示,一带电油滴Q悬浮在平行板电容器两极板A、B之间,处于静止状态.下列做法中,能使 Q仍保持静止的有( )
 如图所示,一带电油滴Q悬浮在平行板电容器两极板A、B之间,处于静止状态.下列做法中,能使 Q仍保持静止的有( )
如图所示,一带电油滴Q悬浮在平行板电容器两极板A、B之间,处于静止状态.下列做法中,能使 Q仍保持静止的有( )| A. | 将极板A向上移一点 | B. | 将极板B向左平移一点 | ||
| C. | 将极板B向下移一点 | D. | 将P向右滑 |
3. 如图所示,直线A为某电源的U-I图线,直线B为某电阻的U-I图线,用该电源、电阻组成闭合电路时,电源的输出功率和电源的效率分别是( )
如图所示,直线A为某电源的U-I图线,直线B为某电阻的U-I图线,用该电源、电阻组成闭合电路时,电源的输出功率和电源的效率分别是( )
 如图所示,直线A为某电源的U-I图线,直线B为某电阻的U-I图线,用该电源、电阻组成闭合电路时,电源的输出功率和电源的效率分别是( )
如图所示,直线A为某电源的U-I图线,直线B为某电阻的U-I图线,用该电源、电阻组成闭合电路时,电源的输出功率和电源的效率分别是( )| A. | 4W,33.3% | B. | 2W,67% | C. | 2W,33.3% | D. | 4W,67% |
10.在国际单位制中关于力学的基本单位正确的一组是( )
| A. | 克、分钟、千米 | B. | 千克、小时、米 | C. | 千克、秒、千米 | D. | 千克、秒、米 |
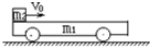 如图所示,质量m1=2kg的小车静止在光滑的水平面上,车长L=90m,现有质量m2=0.5kg可视为质点的物块,以水平向右的速度v0=20m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.4,取g=10m/s2,求:
如图所示,质量m1=2kg的小车静止在光滑的水平面上,车长L=90m,现有质量m2=0.5kg可视为质点的物块,以水平向右的速度v0=20m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.4,取g=10m/s2,求: