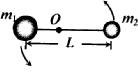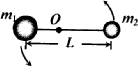题目内容
两颗靠得很近的恒星称为双星,这两颗星必须各以一定的速率绕它们连线上的某一点转动(这一点称为旋转中心),才不至于因万有引力而吸在一起,已知双星的质量之比为mA.:mB=1:2,则它们做圆周运动的半径之比RA:RB=
2:1
2:1
,向心加速度之比aA:aB=2:1
2:1
.分析:“双星”围绕它们连线上的同一点为圆心做匀速圆周运动,运动过程中两者的周期、角速度相同,由对方的万有引力提供向心力,根据牛顿第二定律分别对两星进行列方程求解.
解答:解:设“双星”的角速度为ω,根据牛顿第二定律得
对星A:G
=mAω2RA ①
对星B:G
=mBω2RB ②
由①:②得RA:RB=mB:mA=2:1
向心加速度之比aA:aB=ω2RA:ω2RB=2:1
故答案为:2:1 2:1
对星A:G
| mAmB |
| L2 |
对星B:G
| mAmB |
| L2 |
由①:②得RA:RB=mB:mA=2:1
向心加速度之比aA:aB=ω2RA:ω2RB=2:1
故答案为:2:1 2:1
点评:“双星”是万有引力部分常见的题型,关键抓住“双星”的条件:角速度相同、周期相同,采用隔离法由牛顿第二定律研究.

练习册系列答案
相关题目
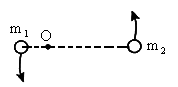
 、
、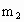 ,相距为L,试求:(1)两颗星转动中心的位置;
,相距为L,试求:(1)两颗星转动中心的位置;