题目内容
如图所示，地面OB段是光滑的，BC段不光滑．B点静止放着一个质量为m的质点Q，另一个质量也为m的质点P靠紧被压缩的弹簧（不连接），并处于静止状态，弹簧的弹性势能是EP．突然释放弹簧，质点P脱离弹簧后与质点Q相碰，碰后粘连在一起滑行至C点停止．若两质点与地面BC段之间的动摩擦因数是μ，求：（1）质点P脱离弹簧时的速度
（2）两质点相碰后的总动能
（3）B、C之间的距离．
【答案】分析：（1）释放弹簧，弹簧的弹性势能转化为质点P的动能，根据机械能守恒求解质点P脱离弹簧时的速度v；
（2）两个碰撞过程，遵守动量守恒定律，由此定律列式求出碰后两个物体的共同速度v′，相碰后的总动能为Ek=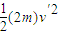
；
（3）两个质点从B到C过程，运用动能定理求解B、C之间的距离．
解答：解：（1）释放弹簧，根据机械能守恒得：EP=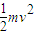
，解得，质点P脱离弹簧时的速度为 v=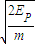
（2）对于两个质点碰撞过程，根据动量守恒得
mv=2mv′
相碰后的总动能为Ek=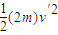
联立解得，相碰后的总动能为Ek=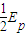
（3）两个质点从B到C过程，由动能定理得
-μ?2mgs=0-Ek，
解得，s=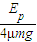
答：
（1）质点P脱离弹簧时的速度为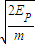
（2）两质点相碰后的总动能为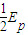
．
（3）B、C之间的距离为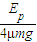
．
点评：本题是含有非弹性碰撞的过程，关键要把握等每个过程遵循的物理规律，运用机械能守恒、动量守恒和动能定理求解．
（2）两个碰撞过程，遵守动量守恒定律，由此定律列式求出碰后两个物体的共同速度v′，相碰后的总动能为Ek=
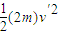；（3）两个质点从B到C过程，运用动能定理求解B、C之间的距离．
解答：解：（1）释放弹簧，根据机械能守恒得：EP=
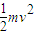，解得，质点P脱离弹簧时的速度为 v=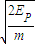（2）对于两个质点碰撞过程，根据动量守恒得
mv=2mv′
相碰后的总动能为Ek=
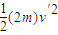
联立解得，相碰后的总动能为Ek=
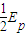
（3）两个质点从B到C过程，由动能定理得
-μ?2mgs=0-Ek，
解得，s=
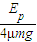
答：
（1）质点P脱离弹簧时的速度为
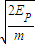
（2）两质点相碰后的总动能为
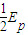．（3）B、C之间的距离为
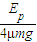．点评：本题是含有非弹性碰撞的过程，关键要把握等每个过程遵循的物理规律，运用机械能守恒、动量守恒和动能定理求解．
练习册系列答案
相关题目
如图所示，一根跨越一固定的水平光滑细杆、轻绳两端拴有两个质量均为m的小球a和b（可视为质点），Oa段的长度为L1，Ob段的长度为L2，且L1＞L2，球a置于地面，球b被拉到与细杆水平的位置，在绳刚拉直时放手，小球b从静止状态向下摆动，当球b摆到最低点时，恰好与球a在同一水平位置发生碰撞并粘合在一起，设碰撞时间极短，往后两球以O点为圆心做圆周运动，若已知碰前瞬间球a的速度大小为va，方向竖直向上，轻绳不可伸长且始终处于绷紧状态，求：
一枚火箭由地面竖直向上发射，其速度-时间图象如图所示，由图可知（ ）
（2004?南京三模）如图所示，一根跨越一固定的水平光滑细杆的轻绳，两端各系一个小球．球a置于地面，球b被拉到与细杆同一水平的位置．在绳刚拉直时放手，使球b从静止状态向下摆动．当摆到Ob段轻绳与竖直方向的夹角为60°时，球a刚要离地，求球a质量与球b质量之比．（已知图中Ob段的长度小于Oa段的长度）
（2010?延庆县一模）如图所示，地面OB段是光滑的，BC段不光滑．B点静止放着一个质量为m的质点Q，另一个质量也为m的质点P靠紧被压缩的弹簧（不连接），并处于静止状态，弹簧的弹性势能是EP．突然释放弹簧，质点P脱离弹簧后与质点Q相碰，碰后粘连在一起滑行至C点停止．若两质点与地面BC段之间的动摩擦因数是μ，求：