题目内容
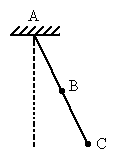
如图所示，在一根长为L的不计质量的细棒中点和末端各连一质量为m的小球，棒可以在竖直平面内绕固定点A转动，将棒拉至某位置后释放，末端C球摆到最低点时，棒C端受到的拉力刚好等于球重的2倍．求：
(1)C球通过最低点时，速度大小是多少？
(2)此时棒AB段受到的拉力是多大？
答案：
解析：
解析：
|
对C球进行受力分析，利用牛顿第二定律，可得到其速度，B球和C球有共同的角速度，进一步得到B球的速度，对B球进行受力分析，利用牛顿第二定律和向心力公式即可计算得出． 当棒到竖直位置时，对C球有： TC－mg＝m 又因为TC＝2 mg 所以vC＝ B球和C球有共同的角速度，由题意知 vB＝ TB－mg－TC＝m 所以TB＝ 所以棒AB端受到的拉力是： TAB＝ |
vC，所以对B球有：
mg＋TC＝
mg
练习册系列答案
相关题目
如图所示，在一根长1.5L的不能伸长的轻绳上，穿一个质量为m的光滑小圆环C，然后把绳的两端固定在竖直轴上，绳的A、B端在竖直轴上的距离为L/2，转动竖直轴带动C环在水平面内做匀速圆周运动，当绳的B端正好在C环的轨道平面上时，求：
如图所示，手持一根长为l的轻绳的一端在水平桌面上做半径为r、角速度为ω的匀速圆周运动，绳始终保持与该圆周相切，绳的另一端系一质量为m的木块，木块也在桌面上做匀速圆周运动，不计空气阻力，下列判断中正确的是（ ）| A、手对木块的拉力做了功 | ||
| B、木块不受桌面的摩擦力 | ||
C、绳的拉力大小等于
| ||
D、手拉木块做功的功率等于
|
