Question

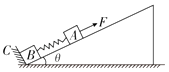
【题目】有一倾角θ=37°的硬杆，其上套有一下端固定于O点，劲度系数为k=100N/m的轻弹簧，弹簧的自由端位于硬杆上的Q处．硬杆OQ部分光滑，PQ部分粗糙，弹簧与杆间无摩擦．一个质量为m=1kg的小球套在此硬杆上，从P点由静止开始滑下，已知小球与硬杆间的动摩擦因数为μ=0.5，PQ间的距离为L=0.91m．弹簧的弹性势能与其形变量x的关系为Ep= kx2 ， 不计空气的阻力做功及小球与弹簧碰撞时的能量损失．（已知g=10m/s2 ， sin 37°=0.6，cos 37°=0.8 ）．求：

（1）小球在运动过程中达到最大速度时弹簧的形变量是多少；
（2）小球在运动过程中所能达到的最大速度vm；
（3）经过较长的时间后，系统能够处于稳定状态．试对这一稳定状态作简单描述．并求出整个过程中因摩擦而产生的热能．

Answer 1

【答案】
（1）

解：当小球从P点无初速滑下时，弹簧被压缩至x处时小球的加速度为零，速度有最大值，因为硬杆OQ部分光滑，则有：

mgsinθ=kx代入数据得：x=0.06m

（2）

解：小球由P点无初速滑下至弹簧被压缩至x=0.06m处的过程中，对小球运用功能关系，有：

mgsinθ（l+x）﹣μmgcosθl﹣W弹=

又 W弹= kx2

即：mgsinθ（l+x）﹣μmgcosθl﹣ kx2=

代入数据得：vm=2m/s

（3）

解：经过较长的时间后，小球将在Q点以下做来回往复式运动，小球的机械能与弹簧的弹性势能相互转化，整个系统处于稳定状态．在不计空气的阻力做功及小球与弹簧碰撞时的能量损失的情况下，全过程中系统的机械能减小量即为整个过程中因摩擦而产生的热能． 有：Q=mglsinθ=5.46J

【解析】（1）当加速度为零时小球的速度最大，由平衡条件和胡克定律结合求弹簧的形变量．（2）小球由P点无初速滑下至弹簧被压缩至最大的过程中，对小球运用功能关系列式，可求得最大速度vm ． （3）经过较长的时间后，小球将在Q点以下做来回往复式运动，小球的机械能与弹簧的弹性势能相互转化，整个系统处于稳定状态．根据能量守恒求．
【考点精析】本题主要考查了功能关系的相关知识点，需要掌握当只有重力（或弹簧弹力）做功时，物体的机械能守恒；重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2；合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 （动能定理）；除了重力（或弹簧弹力）之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1才能正确解答此题．