Question

如图所示，在质量为1kg的重物上系着一条长30cm的细绳，细绳的另一端连着套在水平的棒上可以滑动的圆环，环与棒间的动摩擦因数为0．75．另有一条细绳，在其一端跨过定滑轮，定滑轮固定在距离圆环0．5 m的地方．当细绳的端点挂上重物G，另一端与1kg的重物相连，圆环将要滑动时，试问：

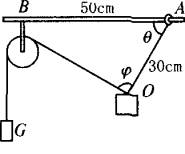
(1)长为30cm的细绳的张力是多少？

(2)圆环将要开始滑动时，重物G的质量是多少？

(3)角φ是多大？

 

Answer 1

答案：
解析：

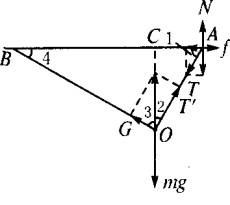
解析：对A、O两点处的物体作受力分析如图所示． 　　对A处的环有：μN＝Tcos∠1①N＝Tsin∠1② 　　由①②得tan∠1＝＝ 　　过O作AB的垂线，则AC＝OAcos∠1＝30×cm＝18cm．OC＝OAsin∠1＝24cm． 　　从而BC＝(50-18)cm＝32cm，tan∠4＝＝＝．因为tan∠4·tan∠1＝1，故∠1与4∠互余，其和为90°．可见∠4＝180°-∠1-∠4＝90°，为直角． 　　(1)对O处物体，有T′＝mgcos∠2＝mgsin∠1＝0．8mg＝8N，即长30cm的细线的张力为8N． 　　(2)绳将要滑动时，由上分析知：G＝mgsin∠2＝0．6kg． 　　(3)由上分析知：∠4＝90°． 　　答案：(1)8N    (2)0．6kg    (3)90° 　　引申：在图示情景下，设O处重物质量为m1，重物G的质量为m2，要维持各物的位置均不变，则m2的质量增加m时，m1的质量至少增加多少? 　　小结：力是矢量，其运算方法满足平行四边形法则和正交分解法则．计算求解时，要先作好图示，然后充分利用几何关系求解．

提示：

先用解析中的方法找出m1、m2的关系的表达式，再依式讨论求解．