题目内容
如图所示，光滑的半圆柱体的半径为R，其上方有一个曲线轨道AB，轨道底端水平并与半圆柱体顶端相切．质量为m的小球沿轨道滑至底端（也就是半圆柱体的顶端）B点时的速度大小为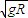
，方向沿水平方向．小球在水平面上的落点为C（图中未标出），则（ ）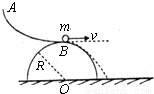
A．小球将沿圆柱体表面做圆周运动滑至C点
B．小球将做平抛运动到达C点
C．OC之间的距离为
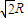
D．OC之间的距离为R
【答案】分析：通过小球在最高点B的受力和速度情况判断小球的运动，根据平抛运动的规律求出OC间的距离．
解答：解：A在最高点B，根据牛顿第二定律有：mg-N=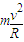
，解得N=0．知小球在最高点B仅受重力，有水平初速度，做平抛运动．故A错误，B正确．
C、根据R=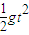
得，t=
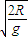，则水平位移x=
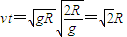．故C正确，D错误．
故选BC．
点评：解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，结合运动学公式进行求解．
解答：解：A在最高点B，根据牛顿第二定律有：mg-N=
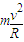，解得N=0．知小球在最高点B仅受重力，有水平初速度，做平抛运动．故A错误，B正确．C、根据R=
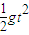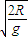得，t=，则水平位移x=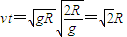．故C正确，D错误．故选BC．
点评：解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，结合运动学公式进行求解．
练习册系列答案
相关题目
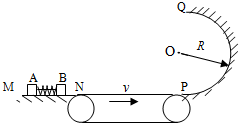如图所示，光滑的水平导轨MN右端N处与水平传送带理想连接，传送带长度L=0.8m，皮带以恒定速率v=3.0m/s向右匀速运动．传送带的右端处平滑连接着一个在竖直平面内、半径为R=0.4m的光滑半圆轨道PQ，两个质量均为m=0.2kg的滑块A、B置于水平导轨MN上，开始时滑块A、B之间用细绳相连，其间有一压缩的轻弹簧，系统处于静止状态．现使细绳断开，弹簧伸展，滑块B脱离弹簧后滑上传送带，从右端滑出并沿半圆轨道运动到最高点Q后水平飞出，又正好落回N点．已知滑块B与传送带之间的动摩擦因数μ=
A．如图所示，光滑的半圆槽内，A球从高h处沿槽自由滑下，与静止在槽底的B球相碰，若碰撞后A球和B球到达的最大高度均为h/9，A球、B球的质量之比为
