题目内容
质量分别为m1和m2的小车A和B放在水平面上,小车A的右端连着一根水平的轻弹簧,处于静止.小车B从右面以某一初速驶来,与轻弹簧相碰,之后,小车A获得的最大速度的大小为v.如果不计摩擦,也不计相互作用过程中的机械能损失.求:(1)小车B的初速度大小.
(2)如果只将小车A、B的质量都增大到原来的2倍,再让小车B与静止小车A相碰,要使A、B小车相互作用过程中弹簧的最大压缩量保持不变,小车B的初速度大小又是多大?

【答案】分析:①两车碰撞过程中,动量与机械能守恒,由动量守恒定律与机械能守恒定律可以求出小车B的初速度v;
②弹簧压缩最短时,弹簧的弹性势能最大,由动量守恒定律与能量守恒定律求解.
解答:解:(1)设小车B开始的速度为v,A、B相互作用后A的速度即A获得的最大速度v,
系统动量守恒m2vo=m1v+m2v2
相互作用前后系统的总动能不变 m2v2=
m2v2= m1v2+
m1v2+ m2v22,
m2v22,
解得:v=4m/s;
解得:v=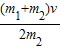
(2)第一次弹簧压缩最短时,A、B有相同的速度,据动量守恒定律,有m2v=(m1+m2)v共,得
v共=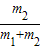 v
v
此时弹簧的弹性势能最大,等于系统总动能的减少
△E= m2v2-
m2v2- (m1+m2)
(m1+m2)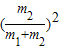
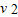 =
=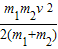
同理,小车A、B的质量都增大到原来的2倍,小车B的初速度设为v3,
A、B小车相互作用过程中弹簧的压缩量最大时,系统总动能减少为△E′=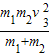
由△E=△E',得
小车B的初速度v3=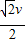 =
=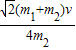
答:(1)小车B的初速度大小是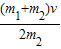 .
.
(2)小车B的初速度大是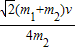
点评:能根据动量守恒条件判断系统动量守恒并能列式求解,能根据机械能守恒条件判断系统机械能守恒并列式求解是解决本题两问的关键
②弹簧压缩最短时,弹簧的弹性势能最大,由动量守恒定律与能量守恒定律求解.
解答:解:(1)设小车B开始的速度为v,A、B相互作用后A的速度即A获得的最大速度v,
系统动量守恒m2vo=m1v+m2v2
相互作用前后系统的总动能不变
 m2v2=
m2v2= m1v2+
m1v2+ m2v22,
m2v22,解得:v=4m/s;
解得:v=
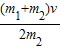
(2)第一次弹簧压缩最短时,A、B有相同的速度,据动量守恒定律,有m2v=(m1+m2)v共,得
v共=
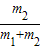 v
v此时弹簧的弹性势能最大,等于系统总动能的减少
△E=
 m2v2-
m2v2- (m1+m2)
(m1+m2)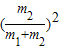
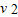 =
=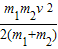
同理,小车A、B的质量都增大到原来的2倍,小车B的初速度设为v3,
A、B小车相互作用过程中弹簧的压缩量最大时,系统总动能减少为△E′=
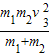
由△E=△E',得
小车B的初速度v3=
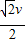 =
=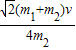
答:(1)小车B的初速度大小是
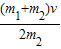 .
.(2)小车B的初速度大是
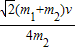
点评:能根据动量守恒条件判断系统动量守恒并能列式求解,能根据机械能守恒条件判断系统机械能守恒并列式求解是解决本题两问的关键

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
两颗行星的质量分别为m1和m2,绕太阳运行的轨道半长轴分别为r1和r2,则它们的公转周期之比为( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
| D、无法确定 |
 一对双星,是由相距L、质量分别为M1和M2的两颗星体构成,两星间引力很大但又未吸引到一起,是因为它们以连线上某点为圆心做圆周运动的结果,如图所示,试求它们各自运转半径和角速度各是多少?
一对双星,是由相距L、质量分别为M1和M2的两颗星体构成,两星间引力很大但又未吸引到一起,是因为它们以连线上某点为圆心做圆周运动的结果,如图所示,试求它们各自运转半径和角速度各是多少? 如图所示,水平放置的金属平行板的B板接地,A板电势为+U,两板间距离为d.d比两板间的尺寸小很多,在两板之间有一长为l的绝缘轻杆,可绕固定轴O在竖直面内无摩擦地自由转动,杆的两端分别连着两个小球1和2,它们的质量分别为m1和m2,m1<m2,它们的带电量分别为-q1和+q2,q1<q2,当杆由图示水平位置从静止开始转到竖直位置时( )
如图所示,水平放置的金属平行板的B板接地,A板电势为+U,两板间距离为d.d比两板间的尺寸小很多,在两板之间有一长为l的绝缘轻杆,可绕固定轴O在竖直面内无摩擦地自由转动,杆的两端分别连着两个小球1和2,它们的质量分别为m1和m2,m1<m2,它们的带电量分别为-q1和+q2,q1<q2,当杆由图示水平位置从静止开始转到竖直位置时( )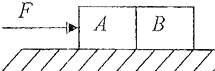 如图所示,质量分别为m1和m2的A、B两物体放置在粗糙水平桌面上,恒力F作用在A物体上,则以下说法正确的是( )
如图所示,质量分别为m1和m2的A、B两物体放置在粗糙水平桌面上,恒力F作用在A物体上,则以下说法正确的是( )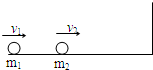 (1)(3-5)在汤姆孙发现电子后,对于原子中正负电荷的分布的问题,科学家们提出了许多模型,最后他们认定:占原子质量绝大部分的正电荷集中在很小的空间范围内,电子绕正电荷旋转.此模型称原子的有核模型.最先提出原子有核模型的科学家是
(1)(3-5)在汤姆孙发现电子后,对于原子中正负电荷的分布的问题,科学家们提出了许多模型,最后他们认定:占原子质量绝大部分的正电荷集中在很小的空间范围内,电子绕正电荷旋转.此模型称原子的有核模型.最先提出原子有核模型的科学家是