题目内容
13. 固定有竖直杆的小车总质量为M,在竖直杆上套一个质量为m的球,已知球与竖直杆之间的动摩擦因数为μ,要使球能沿杆匀速下滑,则对小车施加的水平作用力F=$\frac{1}{μ}$(M+m)g,此时小车的加速度a=$\frac{g}{μ}$(不计地面的摩擦).
固定有竖直杆的小车总质量为M,在竖直杆上套一个质量为m的球,已知球与竖直杆之间的动摩擦因数为μ,要使球能沿杆匀速下滑,则对小车施加的水平作用力F=$\frac{1}{μ}$(M+m)g,此时小车的加速度a=$\frac{g}{μ}$(不计地面的摩擦).
分析 小球竖直方向匀速下滑,水平方向具有与小车相同的加速度.分析小球竖直方向的受力:重力mg和滑动摩擦力f,二力平衡,即可得到滑动摩擦力f,由f=μN,求出杆对小球的力,根据牛顿第二定律求出小球水平方向的加速度,小车与小球水平方向有相同的加速度,即得结果.
解答 解:设小车的加速度为a.
对小球:
竖直方向:受到重力mg和滑动摩擦力f,小球匀速下滑时,则有 f=mg
水平方向:受到杆的弹力N,则有 N=ma,
又f=μN
联立以上三式,得 a=$\frac{g}{μ}$
对整体,根据牛顿第二定律得:
水平方向:F=(M+m)a
解得:F=$\frac{1}{μ}$(M+m)g,
故答案为:F=$\frac{1}{μ}$(M+m)g,a=$\frac{g}{μ}$
点评 本题运用正交分解法研究小球的受力情况,再运用整体法,根据牛顿第二定律即可求解水平力F.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
3.以下说法正确的是( )
| A. | 晶体有固定的熔点,非晶体没有固定的熔点 | |
| B. | 外界对物体做功,物体内能一定增加 | |
| C. | 布朗运动是悬浮在液体中的小颗粒的运动,它说明液体分子永不停息地做无规则热运动 | |
| D. | 当分子间的引力和斥力平衡时,分子势能最小 | |
| E. | 知道水蒸气的摩尔体积和水分子的体积,可计算出阿伏加德罗常数 |
4. 如图所示,四分之一光滑圆弧面AB与倾角为60°的光滑斜面AC顶部相接,A处有一光滑的定滑轮,跨过定滑轮用轻质细绳连接质量分别为m1、m2的两小球,系统静止时连接的绳子与水平方向的夹角为60°.两小球及滑轮大小可忽略,则两小球质量的比值m1:m2为( )
如图所示,四分之一光滑圆弧面AB与倾角为60°的光滑斜面AC顶部相接,A处有一光滑的定滑轮,跨过定滑轮用轻质细绳连接质量分别为m1、m2的两小球,系统静止时连接的绳子与水平方向的夹角为60°.两小球及滑轮大小可忽略,则两小球质量的比值m1:m2为( )
 如图所示,四分之一光滑圆弧面AB与倾角为60°的光滑斜面AC顶部相接,A处有一光滑的定滑轮,跨过定滑轮用轻质细绳连接质量分别为m1、m2的两小球,系统静止时连接的绳子与水平方向的夹角为60°.两小球及滑轮大小可忽略,则两小球质量的比值m1:m2为( )
如图所示,四分之一光滑圆弧面AB与倾角为60°的光滑斜面AC顶部相接,A处有一光滑的定滑轮,跨过定滑轮用轻质细绳连接质量分别为m1、m2的两小球,系统静止时连接的绳子与水平方向的夹角为60°.两小球及滑轮大小可忽略,则两小球质量的比值m1:m2为( )| A. | 1:2 | B. | 3:2 | C. | 2:3 | D. | $\sqrt{3}$:2 |
8.关于机械波,下列说法与事实不一致的是( )
| A. | 能在真空中传播 | B. | 频率由波源决定 | ||
| C. | 能产生干涉、衍射现象 | D. | 在传播过程中能传递能量 |
18.伽利略研究变速运动规律时做了著名的“斜面实验”:他测量了铜球在较小倾角斜面上运动的位移和时间,发现位移与时间的平方成正比,增大斜面倾角,该规律仍然成立.于是,他外推到倾角为90°的情况,得出结论( )
| A. | 自由落体运动是一种匀变速直线运动 | |
| B. | 力是使物体产生加速度的原因 | |
| C. | 力不是维持物体运动的原因 | |
| D. | 物体具有保持原来运动状态的惯性 |
5.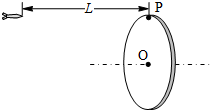 如图所示,一位同学玩飞镖游戏.圆盘最上端有一P点,飞镖抛出时与P等高,且距离P点为L.当飞镖以初速度v0垂直盘面瞄准P点抛出的同时,圆盘以经过盘心O点的水平轴在竖直平面内匀速转动.忽略空气阻力,重力加速度为g,若飞镖恰好击中P点,则( )
如图所示,一位同学玩飞镖游戏.圆盘最上端有一P点,飞镖抛出时与P等高,且距离P点为L.当飞镖以初速度v0垂直盘面瞄准P点抛出的同时,圆盘以经过盘心O点的水平轴在竖直平面内匀速转动.忽略空气阻力,重力加速度为g,若飞镖恰好击中P点,则( )
 如图所示,一位同学玩飞镖游戏.圆盘最上端有一P点,飞镖抛出时与P等高,且距离P点为L.当飞镖以初速度v0垂直盘面瞄准P点抛出的同时,圆盘以经过盘心O点的水平轴在竖直平面内匀速转动.忽略空气阻力,重力加速度为g,若飞镖恰好击中P点,则( )
如图所示,一位同学玩飞镖游戏.圆盘最上端有一P点,飞镖抛出时与P等高,且距离P点为L.当飞镖以初速度v0垂直盘面瞄准P点抛出的同时,圆盘以经过盘心O点的水平轴在竖直平面内匀速转动.忽略空气阻力,重力加速度为g,若飞镖恰好击中P点,则( )| A. | 飞镖击中P点所需的时间为$\frac{L}{{{{v}_0}}}$ | |
| B. | 圆盘的半径可能为$\frac{{g{L^2}}}{{2{v}_0^2}}$ | |
| C. | 圆盘转动角速度的最小值为$\frac{2π{v}_{0}}{L}$ | |
| D. | P点随圆盘转动的线速度可能为$\frac{5πgL}{4{v}_{0}}$ |
2.一束平行光照射在双缝上,在缝后屏上得到干涉条纹,下列说法中正确的是( )

| A. | 增大双缝到屏的距离,条纹间距变大 | |
| B. | 入射光波长变短,光强不变,条纹间距不变 | |
| C. | 入射光频率变化时条纹间距跟着变化 | |
| D. | 在水里做双缝干涉实验,同样条件下的条纹间距会变化 |
 光滑平行金属轨道如图所示,斜轨与水平轨道在bb′处平滑连接(图中未画出),水平轨道处于竖直向上的匀强磁场中,de、d′e′间宽度是bc、b′c′间宽度的2倍,质量、电阻均 相同的金属棒P、Q分别放置于轨道ab、a′b′和de、d′e′段,P棒位于距水平轨道高度为h处,从静止开始无初速释放.已知金属轨道电阻不计,bc、b′c′和de、d′e′轨道足够长,重力加速度为g.求:
光滑平行金属轨道如图所示,斜轨与水平轨道在bb′处平滑连接(图中未画出),水平轨道处于竖直向上的匀强磁场中,de、d′e′间宽度是bc、b′c′间宽度的2倍,质量、电阻均 相同的金属棒P、Q分别放置于轨道ab、a′b′和de、d′e′段,P棒位于距水平轨道高度为h处,从静止开始无初速释放.已知金属轨道电阻不计,bc、b′c′和de、d′e′轨道足够长,重力加速度为g.求: