题目内容
如图所示，坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场，y轴为两种场的分界面，图中虚线为磁场区域的右边界．现有一质量为m，电荷量为-q的带电粒子从电场中坐标位置（-L，0）处，以初速度v0沿x轴正方向开始运动，且已知L=
．
试求：要使带电粒子能穿越磁场区域而不再返回电场中，磁场的宽度d应满足的条件．
m
| ||
| qE |
试求：要使带电粒子能穿越磁场区域而不再返回电场中，磁场的宽度d应满足的条件．
带电粒子在电场中做类平抛运动，设粒子进入磁场时的速度大小为v，速度方向与y轴的夹角为θ，如图所示，则：
vy=
?
=v0
故
v=
=
v0
cosθ=
=
，θ=45°；
粒子在磁场中做匀速圆周运动的半径为：R=
要使带电粒子能穿越磁场区域，磁场的宽度应满足的条件为：d＜（1+cosθ）R
即：d＜
答：要使带电粒子能穿越磁场区域而不再返回电场中，磁场的宽度d应满足的条件为d＜
．
vy=
| qE |
| m |
| L |
| v0 |
故
v=
|
| 2 |
cosθ=
| vy |
| v |
| ||
| 2 |
粒子在磁场中做匀速圆周运动的半径为：R=
| mv |
| qB |
要使带电粒子能穿越磁场区域，磁场的宽度应满足的条件为：d＜（1+cosθ）R
即：d＜
(1+
| ||
| qB |
答：要使带电粒子能穿越磁场区域而不再返回电场中，磁场的宽度d应满足的条件为d＜
(1+
| ||
| qB |
练习册系列答案
相关题目
（2011?青铜峡市一模）如图所示，坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场，y轴为两种场的分界面，图中虚线为磁场区的右边界．现有一质量为m．电量为-q的带电粒子，从电场中的P点以初速度V0沿x轴正方向开始运动，已知P点的坐标为（-L，0）且
（2007?河东区模拟）如图所示，坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场，y轴为两种场的分界面，图中虚线为磁场区域的右边界．现有一质量为m，电荷量为-q的带电粒子从电场中坐标位置（-L，0）处，以初速度v0沿x轴正方向开始运动，且已知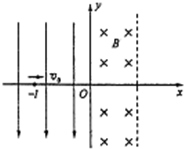
如图所示，坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场，y轴为两种场的分界线，图中虚线为磁场区域的右边界，现有一质量为m、电荷量为-q的带电粒子从电场中坐标位置（-l，0）处，以初速度v0沿x轴正方向开始运动，且已知
（重力不计）。试求：（1）带电粒子进入磁场时速度的大小？