题目内容

为了探测X星球，载着登陆舱的探测飞船总质量为m1在以该星球中心为圆心，半径为r1的圆轨道上运动，周期为T1．随后登陆舱脱离飞船，变轨到离星球更近的半径为r2的圆轨道上运动，此时登陆舱的质量为m2，已知万有引力恒量为G．
求：（1）X星球的质量；
（2）登陆舱在半径为r2的轨道上做圆周运动的周期．
分析：飞船绕星球做圆周运动的向心力由万有引力提供，据此列式求解星球质量M，和周期T．
解答：解：（1）飞船绕X星球圆周运动的向心力由万有引力提供，令X星球的质量为M，则由题意有：
G
m1M
r
2
1
=m1r1
4π2
T
2
1
             ①
解得：M=
4π2
r
3
1
G
T
2
1

（2）登录舱在r2的轨道上运动时满足万有引力提供向心力即：
GMm2
r
2
2
=m2r2
4π2
T
2
2
             ②
联立①和②得：T2=
r
3
2
r
3
1
T1
答：：（1）X星球的质量M=
4π2
r
3
1
G
T
2
1
；
（2）登陆舱在半径为r2的轨道上做圆周运动的周期T2=
r
3
2
r
3
1
T1
点评：万有引力提供圆周运动的向心力G
mM
r2
=mr
4π2
T2
是解决本题的关键
练习册系列答案
相关题目
（2011?浙江）为了探测X星球，载着登陆舱的探测飞船在以该星球中心为圆心，半径为r1的圆轨道上运动，周期为T1．总质量为m1．随后登陆舱脱离飞船，变轨到离星球更近的半径为r2的圆轨道上运动，此时登陆舱的质量为m2则（　　）
为了探测X星球，载着登陆舱的探测飞船在该星球中心为圆心，半径为r1的圆轨道上运动，周期为T1，总质量为m1．随后登陆舱脱离飞船，变轨到离星球更近的半径为r2 的圆轨道上运动，此时登陆舱的质量为m2则X星球的质量为
4π2r
3
1
GT
2
1
4π2r
3
1
GT
2
1
；登陆舱在r1与r2轨道上运动是的速度大小之比为
r2
r1
r2
r1
；若测得X星球表面上方卫星的周期为T0（可以认为卫星轨道半径与X星球半径相等），则X星球的平均密度为
3π
GT
2
0
3π
GT
2
0
．（万有引力恒量为G）
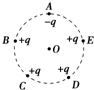为了探测X星球，载着登陆舱的探测飞船在以星球中心为圆心，半径为r1的圆轨道上运动，周期为T1，总质量为m1．随后登陆舱脱离飞船，变轨到离星球更近的半径为r2 的圆轨道上运动，此时登陆舱的质量为m2，则以下结论中（　　）
①X星球的质量为M=
4π2r1
G
T
2
1
          
②X星球表面的重力加速度为gr=
4π2r1
T
2
1

③登陆舱在r1与r2轨道上运动是的速度大小之比为：
v1
v2
=
m1r2
m2r1

④登陆舱在半径为r2轨道上做圆周运动的周期为T2=T1
r
3
2
r
3
1
．
A．为了探测X星球，载着登陆舱的探测飞船在以该星球中心为圆心，半径为r1的圆轨道上运动，周期为T1．随后登陆舱脱离飞船，变轨到离星球更近的半径为r2 的圆轨道上运动．可以得到：X星球的质量M为
 
，登陆舱在半径为r2轨道上做圆周运动的周期T2为
 
．（已知引力常量为G）
B．质量为4.0kg的物体A静止在水平桌面上，另一个质量为2.0kg的物体B以5.0m/s的水平速度与物体A相碰．碰后物体B以1.0m/s的速度反向弹回，则系统的总动量为
 
kg?m/s，碰后物体A的速度大小为
 
m/s．
为了探测X星球，载着登陆舱的探测飞船在以该星球中心为圆心，半径为r1的圆轨道上运动，其总质量为m1，运行周期为T1．随后释放登陆舱脱离飞船，登陆舱变轨到离星球更近的半径为r2的圆轨道上运动，登陆舱的质量为m2，则（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网