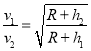题目内容
【题目】一质量为m的物体Q静止于光滑水平地面上，其截面如图所示。图中ab为粗糙的水平面，长度为L；bc为一光滑斜面，斜面和水平面通过与ab和bc均相切的长度可忽略的光滑圆弧连接。现有一质量为m的木块（木块可视为质点）以大小为v0的水平初速度从a点向左运动，在斜面上上升到某一高度后返回，最终在ab上与物体Q相对静止。重力加速度为g。
(1)求木块在ab段的动摩擦因数μ的取值范围；
(2)若取
，求木块在bc段能上升的高度h值（h为木块在bc段距离ab平面的高度）。
【答案】(1)
(2)
【解析】
(1)由动量守恒定律得
恰能回到出发点，由能量守恒得
恰能冲上斜面，由能量守恒得
解得
，
所以木块在ab段的动摩擦因数μ的取值范围为
(2)当
时，则木块在bc段能上升的高度为h，根据动量守恒定律可得
冲上最高点过程，由能量守恒得
得
练习册系列答案
名校课堂系列答案
相关题目
