题目内容
14.汽车发动机的额定功率为40KW,质量为2000kg,当汽车在水平路面上行驶时受到阻力为车重的0.1倍(g=10m/s2),求:(1)汽车在路面上能达到的最大速度?
(2)若汽车以额定功率启动,当汽车速度为10m/s时的加速度?
(3)若汽车从静止开始保持1m/s2的加速度作匀加速直线运动,达到额定输出功率后,汽车保持功率不变又加速行驶了800m,直到获得最大速度后才匀速行驶.求汽车从静止到获得最大行驶速度所用的总时间?
分析 (1)汽车匀速运动时速度最大,由P=Fv求出最大速度.
(2)由P=Fv求出汽车的牵引力,然后由牛顿第二定律求出加速度.
(3)由牛顿第二定律求出匀加速时的牵引力,由P=Fv求出匀加速结束的速度,由匀变速运动直线运动的速度公式求出匀加速的时间;由动能定理求出变加速过程牵引力做功,然后由W=Pt求出变加速的时间,再求出总的运动时间.
解答 解:(1)汽车做匀速直线运动时速度最大,
由平衡条件可知:F=f=0.1mg,
由P=Fv可知,汽车的最大速度:vm=$\frac{P}{F}$=$\frac{P}{0.1mg}$=20m/s;
(2)由P=Fv可知,汽车的牵引力:F1=$\frac{P}{{v}_{1}}$=4000N,
由牛顿第二定律得:F1-f=ma1,a1=1m/s2;
(3)汽车匀加速运动时,由牛顿第二定律的:
F′-0.1mg=ma,F′=4000N,
由P=Fv可知,匀加速解释的速度:v′=$\frac{P}{F′}$=10m/s,
汽车匀加速的运动时间:t1=$\frac{v′}{a}$=10s,
汽车以额定功率加速过程,由动能定理得:
Pt2-0.1mgs=$\frac{1}{2}$mvm2-$\frac{1}{2}$mv′2,时间:t2=37.5s,
汽车总的运动时间:t=t1+t2=47.5s;
答:(1)汽车在路面上能达到的最大速度是20m/s.
(2)若汽车以额定功率启动,当汽车速度为10m/s时的加速度是1m/s2.
(3)汽车从静止到获得最大行驶速度所用的总时间为47.5s.
点评 本题考查了功率公式P=Fv的应用,解决本题的关键知道速度最大时,牵引力与阻力相等,功率不变后,做变加速直线运动,牵引力发生变化,无法通过运动学公式求出变加速运动的时间,通过功率不变,根据动能定理求解变加速运动的时间.

 阅读快车系列答案
阅读快车系列答案
| A. | 甲光对应的光电子的最大初动能小于丙光对应的光电子的最大初动能 | |
| B. | 甲光和乙光的频率相同,且甲光的光强比乙光强 | |
| C. | 丙光的频率比甲、乙光的大,所以光子的能量较大,丙光照射到K极到电子从K极射出的时间间隔明显小于甲、乙光相应的时间间隔 | |
| D. | 用强度相同的甲、丙光照射该光电管,则单位时间内逸出的光电子数相等 |
| A. | 简谐波一定是横波,波上的质点均做简谐运动 | |
| B. | 两个完全相同的振源产生的波相遇时,振动振幅最大的质点是发生了共振 | |
| C. | 在平直公路上一辆警车鸣着笛匀速驶过一站在路边的观察者,警车发出的笛声频率恒定,观察者听到的笛声频率先逐渐变小,后逐渐变大 | |
| D. | 可闻声波比超声波更容易发生明显的衍射,是因为可闻声波的波长比超声波的波长更长 |
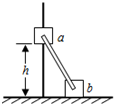 如图所示,滑块a、b的质量均为m,a套在固定光滑竖直杆上,与光滑水平地面相距h,b放在地面上,a、b通过铰链用刚性轻杆连接,不计摩擦,a、b可视为质点,重力加速度大小为g.下列判断正确的是( )
如图所示,滑块a、b的质量均为m,a套在固定光滑竖直杆上,与光滑水平地面相距h,b放在地面上,a、b通过铰链用刚性轻杆连接,不计摩擦,a、b可视为质点,重力加速度大小为g.下列判断正确的是( )| A. | a下落的某段过程中,b对地面的压力可能大于b受到地面的支持力 | |
| B. | a落地前,轻杆对b先做正功后做负功 | |
| C. | a下落的某段过程中,其加速度大小可能大于g | |
| D. | a落地前瞬间a的机械能最小,此时b对地面的压力大小等于mg |
| A. | 匀速圆周运动就是匀速运动 | |
| B. | 匀速圆周运动是一种变加速运动 | |
| C. | 匀速圆周运动的物体处于平衡状态 | |
| D. | 匀速圆周运动的加速度是恒定不变的 |
| A. | 描述一个物体的运动时,参考系可以任意选择.选择不同的参考系来观察同一个物体的运动,其结果可能会有所不同 | |
| B. | 重的物体比轻的物体下落的快,是因为重的物体受到的重力大,加速度大 | |
| C. | 子弹的质量并不重,之所以能对人造成伤害是因为其高速运动时的惯性很大 | |
| D. | 既然作用力和反作用力是大小相等、方向相反的,他们应该互相平衡 |
 如图,一个半径为L的半圆形硬导体AB以速度v在水平U型框架上匀速滑动,匀强磁场的磁感应强度为B,回路电阻为R0,半圆形硬导体AB的电阻为r,其余电阻不计,则半圆形导体AB切割磁感线产生感应电动势的大小及AB之间的电势差分别为( )
如图,一个半径为L的半圆形硬导体AB以速度v在水平U型框架上匀速滑动,匀强磁场的磁感应强度为B,回路电阻为R0,半圆形硬导体AB的电阻为r,其余电阻不计,则半圆形导体AB切割磁感线产生感应电动势的大小及AB之间的电势差分别为( )| A. | 2BLv;$\frac{BLv{R}_{0}}{{R}_{0}+r}$ | B. | 2BLv;BLv | C. | BLv;2BLv | D. | 2BLv;$\frac{2BLv{R}_{0}}{{R}_{0}+r}$ |
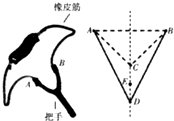 “弹弓”一直是孩子们最喜爱的弹射类玩具之一,其构造如图所示,橡皮筋两端点A、B固定在把手上,橡皮筋ACB恰好处于原长状态,在C处(AB连线的中垂线上)放一固体弹丸,一手执把,另一手将弹丸拉至D点放手,弹丸就会在橡皮筋的作用下迅速发射出去,打击目标,现将弹丸竖直向上发射,已知E是CD中点,则( )
“弹弓”一直是孩子们最喜爱的弹射类玩具之一,其构造如图所示,橡皮筋两端点A、B固定在把手上,橡皮筋ACB恰好处于原长状态,在C处(AB连线的中垂线上)放一固体弹丸,一手执把,另一手将弹丸拉至D点放手,弹丸就会在橡皮筋的作用下迅速发射出去,打击目标,现将弹丸竖直向上发射,已知E是CD中点,则( )| A. | 从D到C,弹丸的机械能守恒 | |
| B. | 从D到C,弹丸的动能一直在增大 | |
| C. | 从D到C,弹丸的机械能先增大后减小 | |
| D. | 从D到E弹丸增加的机械能大于从E到C弹丸增加的机械能 |
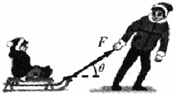 小孩和雪橇的总质量为46kg,在与水平面成37°角的拉力F的作用下,沿水平地面做直线运动,经过0.5s速度由0.3m/s均匀地增加到0.8m/s,已知雪橇与地面的动摩擦因数μ=0.2,求作用力F的大小及地面受到的压力.(取g=10m/s2)
小孩和雪橇的总质量为46kg,在与水平面成37°角的拉力F的作用下,沿水平地面做直线运动,经过0.5s速度由0.3m/s均匀地增加到0.8m/s,已知雪橇与地面的动摩擦因数μ=0.2,求作用力F的大小及地面受到的压力.(取g=10m/s2)