题目内容
6.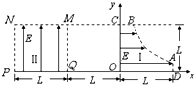 如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在xOy平面的第一象限,存在以x轴y轴及双曲线y=$\frac{{L}^{2}}{4x}$的一段(0≤x≤L,0≤y≤L)的一段 为边界的勻强电场区域I;在第二象限存在以x=-L、x=-2L、y=0,y=L为边界的匀强电场区域Ⅱ(即正方 形MNPQ区域)两个电场大小均为E,电子的电荷量为e,不计电子重力的影响,则 从电场I区域的AB曲线边界由静止释放的各个电子( )
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在xOy平面的第一象限,存在以x轴y轴及双曲线y=$\frac{{L}^{2}}{4x}$的一段(0≤x≤L,0≤y≤L)的一段 为边界的勻强电场区域I;在第二象限存在以x=-L、x=-2L、y=0,y=L为边界的匀强电场区域Ⅱ(即正方 形MNPQ区域)两个电场大小均为E,电子的电荷量为e,不计电子重力的影响,则 从电场I区域的AB曲线边界由静止释放的各个电子( )| A. | 从PN间不同位置处离开区域II | B. | 从PQ间不同位置处离开区域II | ||
| C. | 离开MNPQ的最小动能为$\frac{eEL}{4}$ | D. | 离开MNPQ的最小动能为eEL |
分析 设从AB曲线边界处释放位置坐标为(x,y),再根据动能定理和类平抛运动的分解方法,根据牛顿第二定律求出加速度,由位移公式求出水平位移求出电子从第二象限射出电场的位置.
设从AB曲线边界处释放位置坐标为(x,y),再根据动能定理和类平抛运动的分解方法,求出电子从第二象限射出电场的位置.对全过程应用动能定理,得到电子离开MNPQ时的动能与x的关系,由数学知识求出最小的动能.
解答 解:A、设释放点在电场区域Ⅰ中的坐标为(x,y).在电场Ⅰ中电子被加速,速度为v1时飞离电场Ⅰ,
接着在无电场区域做匀速运动,然后进入电场Ⅱ做类平抛运动,并从NP边离开,运动时间为t2,偏转位移为y2,
由动能定理得:eEx=$\frac{1}{2}$mv12-0,
由匀变速直线运动的位移公式得,偏移量:y2=$\frac{1}{2}$at22=$\frac{1}{2}$$\frac{eE}{m}$$(\frac{L}{{v}_{1}})^{2}$
解得:y2=$\frac{{L}^{2}}{4x}$,所以偏转位移为y2=y,电子将从P点射出.
即在电场Ⅰ区域的AB曲线边界由静止释放的所有电子离开MNPQ时都从P点离开,故AB错误;
CD、由以上的分析可知,电子在两个电场中被加速,w=eEx+eEy,则从B到P由动能定理得:eE(x+y)=Ek-0,
由题意可知:y=$\frac{{L}^{2}}{4x}$,所以只有x=y点释放的电子,离开P点时动能最小,所以x+y=L,即:EKmin=eEL,离开MNPQ的最小动能为eEL,故C错误,D正确;
故选:D.
点评 本题考查了电子在电场中的运动,电子在加速电场中加速,在偏转电场中做类平抛运动,分析清楚电子的运动过程是解题的前提与关键,应用动能定理、类平抛运动规律可以解题.本题中电子先加速后偏转,基本方法是动能定理和运动的分解,难点在于数学知识的应用求极值和轨迹方程.

| A. | 比赛于2012年10月1日下午2点30分开始 | |
| B. | 开场第20秒时,高一队率先进球 | |
| C. | 比赛第30分钟,高二队换人 | |
| D. | 整场比赛共打了60分钟 |
 如图(a)所示为吊式电扇,三个叶片的长度都为l,互成120°中间转动轴半径为r.某同学想用电扇的叶片切割地球磁场来发电供照明用,在叶片外端和内端(即转轴外缘)间用导线连接一电阻为R0的小灯泡,如图(b)所示,若不计所有接触电阻和叶片电阻,电扇匀速转动的角速度为ω.假若电扇所处地球磁场可以认为是匀强磁场,磁感应强度竖直向下分量为B,则下列说法中正确的是( )
如图(a)所示为吊式电扇,三个叶片的长度都为l,互成120°中间转动轴半径为r.某同学想用电扇的叶片切割地球磁场来发电供照明用,在叶片外端和内端(即转轴外缘)间用导线连接一电阻为R0的小灯泡,如图(b)所示,若不计所有接触电阻和叶片电阻,电扇匀速转动的角速度为ω.假若电扇所处地球磁场可以认为是匀强磁场,磁感应强度竖直向下分量为B,则下列说法中正确的是( )| A. | 叶片上b点电势高于a点电势 | |
| B. | 灯两端的电压为Bl(l+r)ω | |
| C. | 通过灯的电流强度为$\frac{Bl(l+r)ω}{2{R}_{0}}$ | |
| D. | 灯泡上消耗电功率为$\frac{{B}^{2}{l}^{2}(l+2r)^{2}{ω}^{2}}{4{R}_{0}}$ |
 如图所示,带正电荷量为q、质量为m的滑块,沿固定绝缘斜面匀速下滑,现加一竖直向上的匀强电场,电场强度为E,且qE≤mg,以下判断中,正确的是( )
如图所示,带正电荷量为q、质量为m的滑块,沿固定绝缘斜面匀速下滑,现加一竖直向上的匀强电场,电场强度为E,且qE≤mg,以下判断中,正确的是( )| A. | 物体将保持匀速下滑 | B. | 物体将沿斜面加速下滑 | ||
| C. | 物体将沿斜面减速下滑 | D. | 不能确定物体的运动状态 |

 如图所示,水平向左的匀强电场中,用长为l的绝缘轻质细绳悬挂一小球,小球质量为m,带电量为+q,将小球拉至竖直位置最低位置A点处无初速释放,小球将向左摆动,细线向左偏离竖直方向的最大角度θ=74°.[$\frac{(1-cosθ)}{sinθ}$=tan($\frac{θ}{2}$)]
如图所示,水平向左的匀强电场中,用长为l的绝缘轻质细绳悬挂一小球,小球质量为m,带电量为+q,将小球拉至竖直位置最低位置A点处无初速释放,小球将向左摆动,细线向左偏离竖直方向的最大角度θ=74°.[$\frac{(1-cosθ)}{sinθ}$=tan($\frac{θ}{2}$)] 如图所示,处于匀强磁场中的两根足够长,电阻不计的光滑平面金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接阻值R=2Ω的电阻匀强磁场方向垂直导轨平面向上,磁感应强度B=1T.质量m=0.2kg,电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触.(sin37°=0.6,cos37°=0.8,g=10m/s2),试求
如图所示,处于匀强磁场中的两根足够长,电阻不计的光滑平面金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接阻值R=2Ω的电阻匀强磁场方向垂直导轨平面向上,磁感应强度B=1T.质量m=0.2kg,电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触.(sin37°=0.6,cos37°=0.8,g=10m/s2),试求 如图所示,一电荷量q=+3×10-5C的小球,用绝缘细线悬挂于竖直放置足够大的平行金属板中的O点.电键S合上后,小球静止时细线与竖直方向的夹角θ=37°.已知两板间距d=0.1m,电源电动势E=15V,内阻r=0.5Ω,电阻R1=3Ω,R2=R3=R4=8Ω,.取g=10m/s2,已知sin37°=0.6,cos37°=0.8.求:
如图所示,一电荷量q=+3×10-5C的小球,用绝缘细线悬挂于竖直放置足够大的平行金属板中的O点.电键S合上后,小球静止时细线与竖直方向的夹角θ=37°.已知两板间距d=0.1m,电源电动势E=15V,内阻r=0.5Ω,电阻R1=3Ω,R2=R3=R4=8Ω,.取g=10m/s2,已知sin37°=0.6,cos37°=0.8.求: