题目内容
5.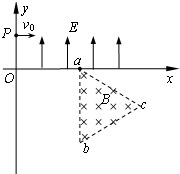 如图所示的平面直角坐标系xoy,在第一象限内有平行于y轴的匀强电场,方向沿y正方向;在第四象限的正三角形abc区域内有匀强磁场,方向垂直于xoy平面向里,正三角形边长为L,且ab边与y轴平行.一质量为m、电荷量为q的粒子,从y轴上的p点(坐标0,h),以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a点(2h,0)进入第四象限,经过磁场后又从y轴上的某点进入第三象限,且速度与y轴负方向成45°角,不计粒子所受的重力.求:
如图所示的平面直角坐标系xoy,在第一象限内有平行于y轴的匀强电场,方向沿y正方向;在第四象限的正三角形abc区域内有匀强磁场,方向垂直于xoy平面向里,正三角形边长为L,且ab边与y轴平行.一质量为m、电荷量为q的粒子,从y轴上的p点(坐标0,h),以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a点(2h,0)进入第四象限,经过磁场后又从y轴上的某点进入第三象限,且速度与y轴负方向成45°角,不计粒子所受的重力.求:(1)电场强度E的大小;
(2)粒子到达a点时速度的大小和方向;
(3)abc区域内磁场的磁感应强度B的最小值.
分析 (1)粒子在电场中做类平抛运动,应用类平抛运动规律求出电场强度.
(2)应用运动的合成与分解求出速度大小与方向.
(3)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出磁感应强度.
解答 解:(1)带电粒子在电场中做类平抛运动,
水平方向:2h=v0t,
竖直方向:h=$\frac{1}{2}$$\frac{qE}{m}$t2,
解得:E=$\frac{m{v}_{0}^{2}}{2qh}$;
(2)粒子到达a点时沿负y方向的分速度为:
vy=at=$\frac{2h}{{t}^{2}}$×t=$\frac{2h}{t}$=v0,
速度:v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{2}$v0, 方向与x轴正方向成450角;
方向与x轴正方向成450角;
(3)粒子在磁场中运动时,由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,
当粒子从b点射出时,半径最大,磁场的磁感应强度有最小值,运动轨迹如图所示:
由几何知识得:r=$\frac{\sqrt{2}}{2}$L,
解得:B=$\frac{2m{v}_{0}}{qL}$;
答:(1)电场强度E的大小为$\frac{m{v}_{0}^{2}}{2qh}$;
(2)粒子到达a点时速度的大小为:$\sqrt{2}$v0,方向:与x轴正方向成450角;
(3)abc区域内磁场的磁感应强度B的最小值为$\frac{2m{v}_{0}}{qL}$.
点评 本题考查了求电场强度、粒子速度、磁感应强度问题,分析清楚粒子运动过程,应用类平抛运动规律、牛顿第二定律即可正确解题,解题时要作出粒子运动轨迹,注意几何知识的应用.

练习册系列答案
相关题目
15.在物理学发展的过程中,有许多伟大的科学家做出了突出贡献.关于科学家和他们的贡献,下列说法正确的是( )
| A. | 英国物理学家焦耳在热学、电磁学等方面做出了杰出贡献,成功地发现了焦耳定律 | |
| B. | 德国天文学家开普勒对他导师第谷观测的行星数据进行多年研究,得出了万有引力定律 | |
| C. | 英国物理学家卡文迪许利用卡文迪许扭秤首先较准确的测定了静电力常量 | |
| D. | 古希腊学者亚里士多德认为物体下落快慢由它们的重量决定,伽利略在他的《两种新科学的对话》中利用逻辑推断使亚里士多德的理论陷入了困境 |
16.关于磁场的方向,下列叙述中不正确的是( )
| A. | 磁感线上每一点的切线方向 | B. | 小磁针北极受力的方向 | ||
| C. | 小磁针静止时北极所指的方向 | D. | 磁铁内部N极到S极的方向 |
20.如图所示,要使Q线圈产生图示方向的电流,可采用的方法有( )


| A. | 闭合电键K 瞬间 | |
| B. | 闭合电键K后,把R的滑片右移 | |
| C. | 闭合电键K后,把P中的铁心从左边抽出 | |
| D. | 闭合电键K后,把Q靠近P |
14.图1中的变压器为理想变压器,原线圈的匝数n1与副线圈的匝数n2之比为5:1.变压器的原线圈接如图2所示的正弦式电流,定值电阻R1=5Ω,R2=15Ω,串联接在副线圈两端.电流表、电压表为理想电表.则( )


| A. | 电流表的读数为0.2A | B. | 电压表V1的读数为100V | ||
| C. | 电压表V2的读数为5V | D. | 电压表V2的读数约为15V |




 中国著名物理学家、中国科学院院士何泽慧教授曾在1945年首次通过实验观察到正、负电子的弹性碰撞过程.有人设想利用电场、磁场控制正、负电子在云室中运动来再现这一过程.实验设计原理如下:在如图所示的xOy平面内,A、C二小孔距原点的距离均为L,每隔一定的时间源源不断地分别从A孔射入正电子,C孔射入负电子,初速度均为v0,方向垂直x轴,正、负电子的质量均为m,电荷量均为e(忽略电子之间的相互作用).在y轴的左侧区域加一水平向右的匀强电场,在y轴的右侧区域加一垂直纸面的匀强磁场(图中未画出),要使正、负电子在y轴上的P(0,L)处相碰.求:
中国著名物理学家、中国科学院院士何泽慧教授曾在1945年首次通过实验观察到正、负电子的弹性碰撞过程.有人设想利用电场、磁场控制正、负电子在云室中运动来再现这一过程.实验设计原理如下:在如图所示的xOy平面内,A、C二小孔距原点的距离均为L,每隔一定的时间源源不断地分别从A孔射入正电子,C孔射入负电子,初速度均为v0,方向垂直x轴,正、负电子的质量均为m,电荷量均为e(忽略电子之间的相互作用).在y轴的左侧区域加一水平向右的匀强电场,在y轴的右侧区域加一垂直纸面的匀强磁场(图中未画出),要使正、负电子在y轴上的P(0,L)处相碰.求: