题目内容
在某介质中形成一列简谐横波,该横波上有相距4m的A、B两点,下图所示为A、B两质点的振动图象,若这列波的波长大于2m,求:这列波的波速.


分析:由振动图象读出周期.由于波的传播方向未知,分两种情况研究:若波由A传到B,B点比A点晚振动,根据波周期性,得出AB间距离与波长的关系,得到波长的通项,结合波长大于2m,得到波长的特殊值,再求出波速.波由B传到A,则A点比B点晚振动的时间.用同样的方法求出波速.
解答:解:由振动图象得:质点振动周期T=0.4s
(1)若波由A传到B,则B点比A点晚振动的时间△t=nT+
T(n=1,2,3,…)
所以A、B间的距离为△s=kλ+
λ(k=0、1、2、3、…)
则波长为λ=
=
因为λ>2m,所以k=0,1
当n=0时,λ1=
m,v1=
=
=
m/s
当n=1时,λ2=
m,v2=
=
=
m/s
(2)若波由B传到A,则A点比B点晚振动的时间△t=nT+
T(n=1,2,3,…)
所以A、B间的距离为△s=kλ+
λ(k=0、1、2、3、…)
则波长为λ=
=
因为λ>2m,所以k=0,1
当n=0时,λ1=16m,v1=
=
=40m/s
当n=1时,λ2=
m,v2=
=
=8m/s
答:若波由A传到B,波速为
m/s或
m/s.若波由B传到A,波速为40m/s或8m/s.
(1)若波由A传到B,则B点比A点晚振动的时间△t=nT+
| 3 |
| 4 |
所以A、B间的距离为△s=kλ+
| 3 |
| 4 |
则波长为λ=
| 4△s |
| 4k+3 |
| 16 |
| 4k+3 |
因为λ>2m,所以k=0,1
当n=0时,λ1=
| 16 |
| 3 |
| λ |
| T |
| 16 |
| 3×0.4 |
| 40 |
| 3 |
当n=1时,λ2=
| 16 |
| 7 |
| λ2 |
| T |
| 16 |
| 7×0.4 |
| 40 |
| 7 |
(2)若波由B传到A,则A点比B点晚振动的时间△t=nT+
| 1 |
| 4 |
所以A、B间的距离为△s=kλ+
| 1 |
| 4 |
则波长为λ=
| 4△s |
| 4k+1 |
| 16 |
| 4k+1 |
因为λ>2m,所以k=0,1
当n=0时,λ1=16m,v1=
| λ |
| T |
| 16 |
| 0.4 |
当n=1时,λ2=
| 16 |
| 5 |
| λ2 |
| T |
| 16 |
| 5×0.4 |
答:若波由A传到B,波速为
| 40 |
| 3 |
| 40 |
| 7 |
点评:本题考查识别、理解振动图象和波动图象联系的能力以及运用数学通项求解特殊值的能力.

练习册系列答案
相关题目
 在某介质中形成一列简谐波,t=0时刻的波形如图中的实线所示.
在某介质中形成一列简谐波,t=0时刻的波形如图中的实线所示.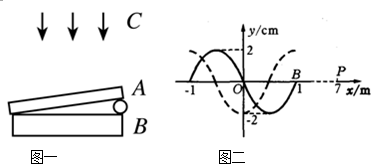
 (物理-选修3-4)
(物理-选修3-4) 在某介质中形成一列简谐波,波向右传播,在0.1s时刻刚好传到B点,波形如图中实线所示,且再经过0.6s,P点也开始起振,求:
在某介质中形成一列简谐波,波向右传播,在0.1s时刻刚好传到B点,波形如图中实线所示,且再经过0.6s,P点也开始起振,求: 在某介质中形成一列简谐横波,t=0时刻的波形如图中的实线所示.若波向右传播,t=0时刻刚好传到A点,且再经过0.6s,P点也开始起振,求:
在某介质中形成一列简谐横波,t=0时刻的波形如图中的实线所示.若波向右传播,t=0时刻刚好传到A点,且再经过0.6s,P点也开始起振,求: