题目内容
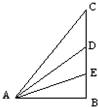
 如图所示光滑斜面CA、DA、EA都以AB为底边.三个斜面的倾角分别为75°、45°、30°.物体分别沿三个斜面由顶端从静止滑到底端,下面说法中正确的是( )
如图所示光滑斜面CA、DA、EA都以AB为底边.三个斜面的倾角分别为75°、45°、30°.物体分别沿三个斜面由顶端从静止滑到底端,下面说法中正确的是( )分析:根据动能定理比较物体到达底端时的速度大小.根据牛顿第二定律,求出物体下滑的加速度,比较出三个斜面哪一个加速度最大,结合运动学公式求出运行的时间,运用数学三角函数关系求出时间最短的斜面倾角.
解答:解:A、根据动能定理得,mgh=
mv2.知高度越高,到达底端的速度越大.故A错误.
B、运动的位移x=
,根据
=
at2得,t=
=
,知当θ=45°时,下滑时间最短.故BC错误,D正确.
故选D.
| 1 |
| 2 |
B、运动的位移x=
| d |
| cosθ |
| d |
| cosθ |
| 1 |
| 2 |
|
|
故选D.
点评:解决本题的关键根据牛顿第二定律求出加速度,根据运动学公式求出运动的时间.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,光滑斜面CA、DA、EA都以AB为底边.三个斜面的倾角分别为75°、45°、30°物体分别沿三个斜面由顶端从静止滑到底端,下面说法中正确的是( )
如图所示,光滑斜面CA、DA、EA都以AB为底边.三个斜面的倾角分别为75°、45°、30°物体分别沿三个斜面由顶端从静止滑到底端,下面说法中正确的是( )| A、物体沿DA滑到底端时具有最大速率 | B、物体沿EA滑到底端所需时间最短 | C、物体沿CA下滑,加速度最大 | D、物体沿CA滑到底端所需时间最短 |
 如图所示,光滑斜面CA、DA、EA都以AB为底边.三个斜面的倾角分别为75°、45°、30°物体分别沿三个斜面由顶端从静止滑到底端,下面说法中正确的是( )
如图所示,光滑斜面CA、DA、EA都以AB为底边.三个斜面的倾角分别为75°、45°、30°物体分别沿三个斜面由顶端从静止滑到底端,下面说法中正确的是( )| A、物体沿CA滑到底端时具有最大速率 | B、物体沿DA滑到底端所需时间最短 | C、物体沿EA下滑过程加速度最大 | D、物体沿三个斜面下滑到底端所需时间相同 |
 如图所示,光滑斜面CA、DA、EA都以AB为底边.三个斜面的倾角分别为75°、45°、30°.物体分别沿三个斜面由顶端从静止滑到底端,下面说法中正确的是( )
如图所示,光滑斜面CA、DA、EA都以AB为底边.三个斜面的倾角分别为75°、45°、30°.物体分别沿三个斜面由顶端从静止滑到底端,下面说法中正确的是( )