Question

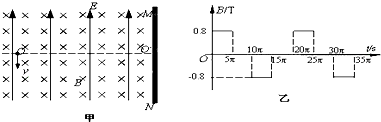（2013?龙江县二模）如图甲所示，竖直挡板MN左侧空间有方向竖直向上的匀强电场和垂直纸面的水平匀强磁场，电场和磁场的范围足够大，电场强度E=40N/C，磁感应强度B随时间t变化的关系如图乙所示，选定磁场垂直纸面向里为正方向，t=0时刻，一质量m=8×10^-4kg、电荷量q=+2×10^-4C的微粒在O点具有竖直向下的速度v=0.12m/s，O′是挡板MN上一点，直线OO′与挡板MN垂直，取g=10m/s²，则微粒下一次经过直线OO′时与O点的距离为（　　）

A．1.2 m

B．0.6 m

C．2.4 m

D．1.8 m

Answer 1

分析：微粒所受电场力和重力平衡，知微粒先在磁场中做匀速圆周运动，根据洛伦兹力提供向心力求出轨道半径和周期的大小，确定出在5πs内转过半个圆周，从而求出微粒再次经过直线OO′时与O点的距离．

解答：解：由题意可知，微粒所受的重力为：G=mg=8×10^-4×10=8×10^-3N
电场力大小为：F=Eq=40×2×10^-4=8×10^-3N
因此重力与电场力平衡．                  
微粒先在洛伦兹力作用下做匀速圆周运动，洛伦兹力提供向心力，则有：
qvB=

mv2

R

解得：R=

mv

qB

=

8×10-4×0.12

2×10-4×40

m=0.6m          
由T=

2πR

v

=

2π×0.6

0.12

s
解得：T=10πs                 
则微粒在5πs内转过半个圆周，再次经直线OO?时与O点的距离为：l=2R=1.2m    
故选：A

点评：本题是力学与电学综合题，根据匀速圆周运动的规律与几何关系相结合，同时运用力学与电学的知识来解题，从而培养学生分析问题的方法，提升解题的能力．